 θετικοί πραγματικοί αριθμοί με
θετικοί πραγματικοί αριθμοί με  . Έστω επίσης
. Έστω επίσης  .
.Θεωρούμε τη συνάρτηση

Να ορίσετε συνεχή συνάρτηση
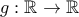 τέτοια, ώστε
τέτοια, ώστε 
Συντονιστής: R BORIS
 θετικοί πραγματικοί αριθμοί με
θετικοί πραγματικοί αριθμοί με  . Έστω επίσης
. Έστω επίσης  .
.
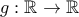 τέτοια, ώστε
τέτοια, ώστε 
Για κατάλληλα μεγάλοBAGGP93 έγραψε:Ας είναιθετικοί πραγματικοί αριθμοί με
. Έστω επίσης
.
Θεωρούμε τη συνάρτηση
Να ορίσετε συνεχή συνάρτησητέτοια, ώστε
 παίρνουμε
παίρνουμε  στο
στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) , ευθεία (μεγάλης κλίσης) από το
, ευθεία (μεγάλης κλίσης) από το  στο
στο  , και όμοια από το
, και όμοια από το 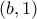 στο
στο  και τέλος,
και τέλος,  έξω από αυτά. Είναι προφανές ότι η
έξω από αυτά. Είναι προφανές ότι η  κάνει την δουλειά. Ο λόγος είναι διότι το παραπάνω ολοκλήρωμα είναι ίσο με το εμβαδόν δύο στενών τριγώνων. Όποιος δεν το βλέπει ας κάνει το σχήμα, για να δει το προφανές.
κάνει την δουλειά. Ο λόγος είναι διότι το παραπάνω ολοκλήρωμα είναι ίσο με το εμβαδόν δύο στενών τριγώνων. Όποιος δεν το βλέπει ας κάνει το σχήμα, για να δει το προφανές.![\displaystyle{\left[a-\delta,b+\delta\right]} \displaystyle{\left[a-\delta,b+\delta\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e23ef97ed43aa3102e48f65427ef5f77.png) όπως και εσείς.
όπως και εσείς. που επιλέξατε είναι τέτοιο, ώστε
που επιλέξατε είναι τέτοιο, ώστε  .
.Ναι, το έκανα μεBAGGP93 έγραψε: Υποψιάζομαι ότι τοπου επιλέξατε είναι τέτοιο, ώστε
.
 ώστε να φανεί ότι το παραπάνω ολοκλήρωμα γίνεται όσο μικρό θέλουμε: Είναι δύο μακρόστενα τρίγωνα ύψους
ώστε να φανεί ότι το παραπάνω ολοκλήρωμα γίνεται όσο μικρό θέλουμε: Είναι δύο μακρόστενα τρίγωνα ύψους  και βάσης
και βάσης 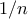 (άρα το ολοκλήρωμα τείνει στο
(άρα το ολοκλήρωμα τείνει στο  )
)Ακριβώς Ευάγγελε.BAGGP93 έγραψε:Καλημέρα σε όλους.
Κύριε Σταύρο, όπως αυτό που μου είχατε απαντήσει :
viewtopic.php?f=9&t=56653#p272661
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης