![f:[0, 1] \rightarrow \mathbb{R} f:[0, 1] \rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/ecfcba9a31408f049a2a93da7b920c8d.png) μία συνεχής συνάρτηση με
μία συνεχής συνάρτηση με  και τέτοια ώστε
και τέτοια ώστε Αποδείξατε ότι υπάρχει
Αποδείξατε ότι υπάρχει  τέτοιο ώστε
τέτοιο ώστε  .
. -- (15, 0);
\end{tikzpicture} \begin{tikzpicture}
\draw [very thick](-5, 0) -- (15, 0);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/8f362567e60cfbafa1f2e381dac662ff.png)
Παλιότερο σχετικό θέμα εδώ.
Συντονιστής: R BORIS
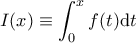 και
και  . Τότε, με ολοκλήρωση κατά μέρη, το δεδομένο μάς λέει ότι
. Τότε, με ολοκλήρωση κατά μέρη, το δεδομένο μάς λέει ότι  .
. . Ισχύει
. Ισχύει  . Επίσης, με διαδοχικά de l'Hospital, βλέπουμε ότι
. Επίσης, με διαδοχικά de l'Hospital, βλέπουμε ότι  .
. για κάποιο
για κάποιο  . Έχουμε
. Έχουμε  , οπότε
, οπότε  . Αλλά επίσης
. Αλλά επίσης  (κατά μέρη) και έτσι
(κατά μέρη) και έτσι  που είναι το ζητούμενο.
που είναι το ζητούμενο. για
για 
 και με de L Hospital
και με de L Hospital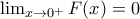
 μπορούμε να εφαρμόσουμε Rolle.
μπορούμε να εφαρμόσουμε Rolle.
 είναι ουσιαστική και δεν μπορεί να παραληφθεί.
είναι ουσιαστική και δεν μπορεί να παραληφθεί. έγινε έτσι ώστε να χρησιμοποιηθεί η συνθήκη
έγινε έτσι ώστε να χρησιμοποιηθεί η συνθήκη 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες