
1/lnx
Συντονιστής: R BORIS
- Tolaso J Kos
- Δημοσιεύσεις: 5226
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Re: 1/lnx
Ισχύει ότιντεχι έγραψε:Να υπολογιστεί το όριο:
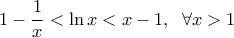 οπότε
οπότε  .
.Όμως:
![\displaystyle{\int_{x}^{x^2} \frac{t}{t-1}\, {\rm d}t= \left [ t + \ln (t-1) \right ]_x^{x^2} = x^2+\ln (x^2-1) - x - \ln (x-1) =x^2 + \ln (x+1) -x} \displaystyle{\int_{x}^{x^2} \frac{t}{t-1}\, {\rm d}t= \left [ t + \ln (t-1) \right ]_x^{x^2} = x^2+\ln (x^2-1) - x - \ln (x-1) =x^2 + \ln (x+1) -x}](/forum/ext/geomar/texintegr/latexrender/pictures/7774118a56f3c5d027459570e270ec4d.png) και
και![\displaystyle{\int_{x}^{x^2}\frac{t^2}{t-1}\, {\rm d}t =\frac{1}{2}\left [ x\left ( x^3+x-2 \right )+ 2 \ln (x+1) \right ]} \displaystyle{\int_{x}^{x^2}\frac{t^2}{t-1}\, {\rm d}t =\frac{1}{2}\left [ x\left ( x^3+x-2 \right )+ 2 \ln (x+1) \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/f25e582ea6246b13afd5f716f4da582b.png)
Οπότε παίρνοντας όρια (προσοχή: το
 όταν παίρνουμε όρια γίνεται
όταν παίρνουμε όρια γίνεται  ) και χρησιμοποιώντας το κριτήριο παρεμβολής βλέπουμε πως το ζητούμενο όριο ισούται με
) και χρησιμοποιώντας το κριτήριο παρεμβολής βλέπουμε πως το ζητούμενο όριο ισούται με  .
.Υ.Σ: Μήπως εννοούσες όμως το όριο
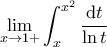 ;
;Η φαντασία είναι σημαντικότερη από τη γνώση !


- exdx
- Επιμελητής
- Δημοσιεύσεις: 1741
- Εγγραφή: Κυρ Δεκ 21, 2008 6:00 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: 1/lnx
Καλησπέρα σε όλους
Στο πνεύμα του Αποστόλη αλλά με πιο αναλυτικές πράξεις
H εφαπτομένη της στο σημείο
στο σημείο  είναι η
είναι η και λόγω της κυρτότητας της f ισχύει ότι
και λόγω της κυρτότητας της f ισχύει ότι  .
.
Για x >1 θα ισχύει ότι και ακόμη αν αντικαταστήσουμε στην (1) όπου x το
και ακόμη αν αντικαταστήσουμε στην (1) όπου x το  θα ισχύει ότι :
θα ισχύει ότι :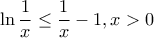 ή
ή 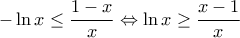 , οπότε για
, οπότε για  θα ισχύει ότι :
θα ισχύει ότι :  , κι έτσι τελικά θα έχουμε για
, κι έτσι τελικά θα έχουμε για  ότι :
ότι : 
και αφού για ισχύει και
ισχύει και  , ολοκληρώνοντας την (2) προκύπτει ότι :
, ολοκληρώνοντας την (2) προκύπτει ότι :  . Όμως
. Όμως
![\displaystyle{\begin{array}{l}
\int\limits_x^{{x^2}} {\frac{t}{{t - 1}}dt} = \int\limits_x^{{x^2}} {\frac{{t - 1 + 1}}{{t - 1}}dt} = \left[ {t + \ln \left| {t - 1} \right|} \right]_x^{{x^2}} = \\
\\
= {x^2} + \ln \left| {{x^2} - 1} \right| - x - \ln \left| {x - 1} \right| = {x^2} - x + \ln \left| {x + 1} \right| \\
\end{array}} \displaystyle{\begin{array}{l}
\int\limits_x^{{x^2}} {\frac{t}{{t - 1}}dt} = \int\limits_x^{{x^2}} {\frac{{t - 1 + 1}}{{t - 1}}dt} = \left[ {t + \ln \left| {t - 1} \right|} \right]_x^{{x^2}} = \\
\\
= {x^2} + \ln \left| {{x^2} - 1} \right| - x - \ln \left| {x - 1} \right| = {x^2} - x + \ln \left| {x + 1} \right| \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/b0044cc1dce0218fae3d6c195201f73e.png)
και
![\displaystyle{\left[ \frac{{{t}^{2}}}{2}+t+\ln \left| t-1 \right| \right]_{x}^{{{x}^{2}}}=\frac{{{x}^{4}}}{2}+{{x}^{2}}-\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|=\frac{{{x}^{4}}}{2}+\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|} \displaystyle{\left[ \frac{{{t}^{2}}}{2}+t+\ln \left| t-1 \right| \right]_{x}^{{{x}^{2}}}=\frac{{{x}^{4}}}{2}+{{x}^{2}}-\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|=\frac{{{x}^{4}}}{2}+\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|}](/forum/ext/geomar/texintegr/latexrender/pictures/db4c213fabedd5bf6e7e9081846f816c.png) .
.
Τελικά ισχύει ότι :
και επειδή : ,
,
θα είναι σύμφωνα με το κριτήριο παρεμβολής :
Υ.Γ Το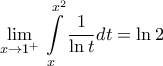 και πάλι
και πάλι
Στο πνεύμα του Αποστόλη αλλά με πιο αναλυτικές πράξεις
H εφαπτομένη της
 στο σημείο
στο σημείο  είναι η
είναι η και λόγω της κυρτότητας της f ισχύει ότι
και λόγω της κυρτότητας της f ισχύει ότι  .
. Για x >1 θα ισχύει ότι
 και ακόμη αν αντικαταστήσουμε στην (1) όπου x το
και ακόμη αν αντικαταστήσουμε στην (1) όπου x το  θα ισχύει ότι :
θα ισχύει ότι :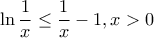 ή
ή 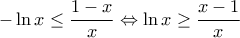 , οπότε για
, οπότε για  θα ισχύει ότι :
θα ισχύει ότι :  , κι έτσι τελικά θα έχουμε για
, κι έτσι τελικά θα έχουμε για  ότι :
ότι : 
και αφού για
 ισχύει και
ισχύει και  , ολοκληρώνοντας την (2) προκύπτει ότι :
, ολοκληρώνοντας την (2) προκύπτει ότι :  . Όμως
. Όμως![\displaystyle{\begin{array}{l}
\int\limits_x^{{x^2}} {\frac{t}{{t - 1}}dt} = \int\limits_x^{{x^2}} {\frac{{t - 1 + 1}}{{t - 1}}dt} = \left[ {t + \ln \left| {t - 1} \right|} \right]_x^{{x^2}} = \\
\\
= {x^2} + \ln \left| {{x^2} - 1} \right| - x - \ln \left| {x - 1} \right| = {x^2} - x + \ln \left| {x + 1} \right| \\
\end{array}} \displaystyle{\begin{array}{l}
\int\limits_x^{{x^2}} {\frac{t}{{t - 1}}dt} = \int\limits_x^{{x^2}} {\frac{{t - 1 + 1}}{{t - 1}}dt} = \left[ {t + \ln \left| {t - 1} \right|} \right]_x^{{x^2}} = \\
\\
= {x^2} + \ln \left| {{x^2} - 1} \right| - x - \ln \left| {x - 1} \right| = {x^2} - x + \ln \left| {x + 1} \right| \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/b0044cc1dce0218fae3d6c195201f73e.png)
και

![\displaystyle{\left[ \frac{{{t}^{2}}}{2}+t+\ln \left| t-1 \right| \right]_{x}^{{{x}^{2}}}=\frac{{{x}^{4}}}{2}+{{x}^{2}}-\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|=\frac{{{x}^{4}}}{2}+\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|} \displaystyle{\left[ \frac{{{t}^{2}}}{2}+t+\ln \left| t-1 \right| \right]_{x}^{{{x}^{2}}}=\frac{{{x}^{4}}}{2}+{{x}^{2}}-\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|=\frac{{{x}^{4}}}{2}+\frac{{{x}^{2}}}{2}-x+\ln \left| x+1 \right|}](/forum/ext/geomar/texintegr/latexrender/pictures/db4c213fabedd5bf6e7e9081846f816c.png) .
.Τελικά ισχύει ότι :

και επειδή :
 ,
, θα είναι σύμφωνα με το κριτήριο παρεμβολής :

Υ.Γ Το
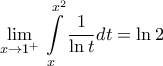 και πάλι
και πάλιKαλαθάκης Γιώργης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες
