 έχει
έχει  παραγώγους σε κάθε σημείο του
παραγώγους σε κάθε σημείο του  . Δείξατε ότι για κάθε ζευγάρι πραγματικών αριθμών
. Δείξατε ότι για κάθε ζευγάρι πραγματικών αριθμών  με
με  και
και
υπάρχει
 τέτοιο ώστε
τέτοιο ώστε  .
.Edit: Δημήτρη ( dement ) ευχαριστώ για το σκούντηγμα.
Συντονιστής: KAKABASBASILEIOS
 έχει
έχει  παραγώγους σε κάθε σημείο του
παραγώγους σε κάθε σημείο του  . Δείξατε ότι για κάθε ζευγάρι πραγματικών αριθμών
. Δείξατε ότι για κάθε ζευγάρι πραγματικών αριθμών  με
με  και
και
 τέτοιο ώστε
τέτοιο ώστε  .
.
 φορές παραγωγίσιμη συνάρτηση
φορές παραγωγίσιμη συνάρτηση  , έστωσαν
, έστωσαν  ,
,  , για τους οποίους ισχύει:
, για τους οποίους ισχύει:
 ,
,  , είναι παραγωγίσιμη στο διάστημα
, είναι παραγωγίσιμη στο διάστημα ![\left[{\alpha,\beta}\right] \left[{\alpha,\beta}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/4473d4d763c4b2d5e3abeb70287d4022.png) με παράγωγο
με παράγωγο

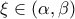 , τέτοιος ώστε να ισχύει:
, τέτοιος ώστε να ισχύει: 

 υπάρχει θέμα με το πρόσημο του
υπάρχει θέμα με το πρόσημο του  που πρέπει να είναι θετικό. Ίσως αντιμετωπίζεται, μιας και σε διαστήματα μπορούμε να εξασφαλίσουμε ότι
που πρέπει να είναι θετικό. Ίσως αντιμετωπίζεται, μιας και σε διαστήματα μπορούμε να εξασφαλίσουμε ότι  , αλλά μια λύση που αντιμετωπίζει επαρκώς το πιθανό πρόβλημα είναι η εξής:
, αλλά μια λύση που αντιμετωπίζει επαρκώς το πιθανό πρόβλημα είναι η εξής: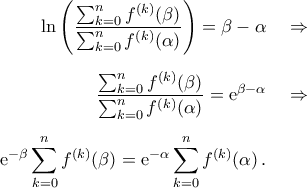
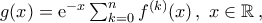 πληρεί τις συνθήκες του θεωρήματος Rolle και, επομένως, υπάρχει
πληρεί τις συνθήκες του θεωρήματος Rolle και, επομένως, υπάρχει  , έτσι ώστε
, έτσι ώστε 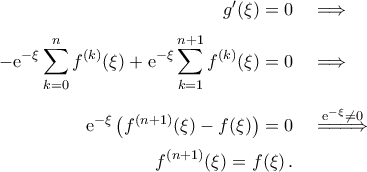

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες