Για σας.
Μου προκάλεσε ενδιαφέρον το θέμα "Διερευνητική" και θέλω να διατυπώσω κάποιες σκέψεις.
Στο βιβλίο " Άλγεβρα Β" δίνεται ο αριθμός e ως το όριο στο άπειρο της αύξουσας ακολουθίας
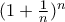
απ' όπου προφανώς είναι

Εδώ για έναν καλό εκπαιδευτικό είναι χρυσή ευκαιρία να δώσει και τον αριθμό

σαν το όριο στο άπειρο της αύξουσας ακολουθίας
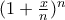
με χ>0 οπότε
είναι επίσης

. Νομίζω μοναδική ευκαιρία.
Στο προκείμενο θέμα ζητιέται μια, στο περίπου, απάντηση η οποία θα μπορούσε να στοιχειοθετηθεί ως εξής:
Έστω

και

ακέραιοι με

>

. Τότε
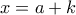
οπότε για να είναι

.
Όμως επειδή
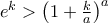
αρκεί να είναι
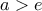
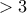
.
Έτσι θα μπορούσαμε να έχουμε τη εξής (σωστή αλλά όχι πλήρη) εικασία. Ότι δηλαδή για ακεραίους

και

με
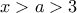
είναι
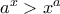
και να γενικεύσουμε.
Για ένα μαθητή Β Λυκείου συνηγορούν υπέρ της εικασίας αυτής ασκήσεις του τύπου

ή

(τελευταία ομάδας Β σχ βιβλ παράγρ 4.1)
Είναι προφανές ότι μια σωστή αντιμετώπιση του θέματος επιτυγχάνεται με τη μελέτη της συναρτήσεως

ως προς το πρόσημό της για τα διάφορα

. Είναι σχετικά εύκολη αλλά μακροσκελής
και αν υπάρχει ενδιαφέρον να την αναρτήσω.
Ευχαριστίες.

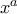

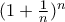 απ' όπου προφανώς είναι
απ' όπου προφανώς είναι 

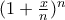 με χ>0 οπότε
με χ>0 οπότε . Νομίζω μοναδική ευκαιρία.
. Νομίζω μοναδική ευκαιρία. και
και  ακέραιοι με
ακέραιοι με 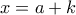 οπότε για να είναι
οπότε για να είναι  .
.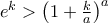 αρκεί να είναι
αρκεί να είναι 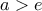
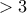 .
.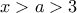 είναι
είναι 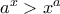 και να γενικεύσουμε.
και να γενικεύσουμε. ή
ή (τελευταία ομάδας Β σχ βιβλ παράγρ 4.1)
(τελευταία ομάδας Β σχ βιβλ παράγρ 4.1) ως προς το πρόσημό της για τα διάφορα
ως προς το πρόσημό της για τα διάφορα