![\displaystyle{f\,,g:\left[a,b\right]\to \left(0,+\infty\right)} \displaystyle{f\,,g:\left[a,b\right]\to \left(0,+\infty\right)}](/forum/ext/geomar/texintegr/latexrender/pictures/c4ceb72cc15f6492595c7425b846ef4b.png) με
με ![\displaystyle{f(x)<g(x)\,,\forall\,x\in\left[a,b\right]} \displaystyle{f(x)<g(x)\,,\forall\,x\in\left[a,b\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b5a166f27ec753101a523586cd42e889.png) .
.Να δείξετε ότι υπάρχει
 τέτοιο, ώστε
τέτοιο, ώστε ![\displaystyle{c\,f(x)\leq g(x)\,,\forall\,x\in\left[a,b\right]} \displaystyle{c\,f(x)\leq g(x)\,,\forall\,x\in\left[a,b\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/f8f638ae7f9084bab3a3b6b27cda4393.png) .
.Συντονιστής: m.pαpαgrigorakis
Η συνάρτησηBAGGP93 έγραψε:Έστωσαν οι συνεχείς συναρτήσειςμε
.
Να δείξετε ότι υπάρχειτέτοιο, ώστε
.
![h: [a,b]\to \mathbb{R} h: [a,b]\to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/0c4468cd42584e23a44c3ccfaebd4eac.png) με
με  είναι καλώς ορισμένη, συνεχής ως πηλίκο συνεχών με
είναι καλώς ορισμένη, συνεχής ως πηλίκο συνεχών με  για κάθε
για κάθε ![x\in [a,b]. x\in [a,b].](/forum/ext/geomar/texintegr/latexrender/pictures/f4385490b1258f3a845e89968e880d59.png)
 σε κάποιο σημείο
σε κάποιο σημείο ![\xi \in [a,b]. \xi \in [a,b].](/forum/ext/geomar/texintegr/latexrender/pictures/8caa2cb41805ea4e6097ede4f0f3652c.png)
Αλλιώς (αν και στην πραγματικότητα δεν πρόκειται για άλλη λύση αλλά παραλλαγή της λύσης του Αχιλλέα).BAGGP93 έγραψε:Έστωσαν οι συνεχείς συναρτήσειςμε
.
Να δείξετε ότι υπάρχειτέτοιο, ώστε
.
 να παίρνει την τιμή
να παίρνει την τιμή  ή και αρνητικές. Συγκεκριμένα, αν η
ή και αρνητικές. Συγκεκριμένα, αν η  έπαιρνε μόνο τιμές
έπαιρνε μόνο τιμές  , το αποτέλεσμα είναι άμεσο. Οπότε ας υποθέσουμε ότι παίρνει και κάποια θετική τιμή. Τότε:
, το αποτέλεσμα είναι άμεσο. Οπότε ας υποθέσουμε ότι παίρνει και κάποια θετική τιμή. Τότε: είναι συνεχής σε κλειστό διάστημα, έχει ελάχιστη τιμή
είναι συνεχής σε κλειστό διάστημα, έχει ελάχιστη τιμή 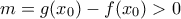 . Αντίστοιχα η
. Αντίστοιχα η  έχει μέγιστη τιμή
έχει μέγιστη τιμή  . 'Αρα για κάθε
. 'Αρα για κάθε 
 .
.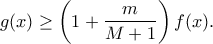
Οι προυποθέσεις μπορούν να εξασθενήσουν και το συμπέρασμα να ενισχυθεί.BAGGP93 έγραψε:Έστωσαν οι συνεχείς συναρτήσειςμε
.
Να δείξετε ότι υπάρχειτέτοιο, ώστε
.
![f,g:[a,b]\rightarrow \mathbb{R} f,g:[a,b]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/99edc50ed57090a234ce3ed765509ca7.png) είναι συνεχείς και
είναι συνεχείς και ![x\in [a,b]\Rightarrow g(x)> f(x) x\in [a,b]\Rightarrow g(x)> f(x)](/forum/ext/geomar/texintegr/latexrender/pictures/9290d5ecc1581f465a16d6f82a34cb7d.png)

![x\in [a,b]\Rightarrow g(x)>c f(x) x\in [a,b]\Rightarrow g(x)>c f(x)](/forum/ext/geomar/texintegr/latexrender/pictures/4b8293f1131bffcae92dda3408789ef1.png)
Σωστά.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: Οι προυποθέσεις μπορούν να εξασθενήσουν και το συμπέρασμα να ενισχυθεί.
Συγκεκριμένα.
Ανείναι συνεχείς και
τότε υπάρχει
ώστε
 αλλά θα μπορούσα να είχα γράψει
αλλά θα μπορούσα να είχα γράψει  ).
).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες