 και
και 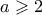 , να αποδειχθεί ότι
, να αποδειχθεί ότι 
Συντονιστές: vittasko, achilleas, emouroukos
Μη αναγνωσμένη δημοσίευση από grigkost » Τρί Δεκ 25, 2012 3:51 pm
 και
και 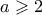 , να αποδειχθεί ότι
, να αποδειχθεί ότι 

Μη αναγνωσμένη δημοσίευση από Demetres » Τετ Δεκ 26, 2012 11:17 am
![f:[0,1] \to \mathbb{R} f:[0,1] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/d961f003d1b32deb05785be107ca82fb.png) με τύπο
με τύπο 
![\displaystyle{ f'(x) = \frac{a}{2}\left[x^{a-1} - \left( \frac{1+x}{2} \right)^{a-1} + \left( \frac{1-x}{2} \right)^{a-1} \right]} \displaystyle{ f'(x) = \frac{a}{2}\left[x^{a-1} - \left( \frac{1+x}{2} \right)^{a-1} + \left( \frac{1-x}{2} \right)^{a-1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/2b6ad9103bcd4e655820aafc3f3f7db6.png)
![\displaystyle{= \frac{a}{2}\left( \frac{1+x}{2} \right)^{a-1}\left[\left(\frac{2x}{1+x}\right)^{a-1} + \left( \frac{1-x}{1+x} \right)^{a-1} - 1 \right]. } \displaystyle{= \frac{a}{2}\left( \frac{1+x}{2} \right)^{a-1}\left[\left(\frac{2x}{1+x}\right)^{a-1} + \left( \frac{1-x}{1+x} \right)^{a-1} - 1 \right]. }](/forum/ext/geomar/texintegr/latexrender/pictures/0baeac2b5c2cbbd986f201b202ed7fa1.png)
 , ο όρος στις αγκύλες είναι το πολύ
, ο όρος στις αγκύλες είναι το πολύ 
 είναι φθίνουσα στο
είναι φθίνουσα στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) . Τέλος επειδή
. Τέλος επειδή  , το αποτέλεσμα έπεται.
, το αποτέλεσμα έπεται.Επιστροφή σε “Θέματα για Λύκειο - Seniors”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off