 συνάρτηση τέτοια ώστε για κάθε
συνάρτηση τέτοια ώστε για κάθε  να ισχύει:
να ισχύει: 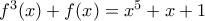 .
.α) δείξετε ότι
 συνεχής στο
συνεχής στο 
β) Να δείξετε ότι υπάρχει ένα τουλάχιστον κοινό σημείο της
 και της y=x στο διάστημα (-2,-1).
και της y=x στο διάστημα (-2,-1).Συντονιστές: m.pαpαgrigorakis, Καρδαμίτσης Σπύρος, Πρωτοπαπάς Λευτέρης, R BORIS, KAKABASBASILEIOS, Μπάμπης Στεργίου
 συνάρτηση τέτοια ώστε για κάθε
συνάρτηση τέτοια ώστε για κάθε  να ισχύει:
να ισχύει: 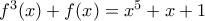 .
. συνεχής στο
συνεχής στο 
 και της y=x στο διάστημα (-2,-1).
και της y=x στο διάστημα (-2,-1).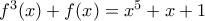 (1)
(1) συνεχής στο [-2,-1].
συνεχής στο [-2,-1].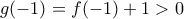

 .
.
 .
. αλλά δεν κατάληξε κάπου
αλλά δεν κατάληξε κάπου...Καλημέρα
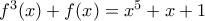 και
και 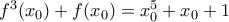 με αφαίρεση
με αφαίρεση  (ταυτότητες…)
(ταυτότητες…)
 και
και 


![\lim_{x\rightarrow a}\left [ f^{3}(x) \right+f(x) -f^{3}(a)-f(a)]=0 \Rightarrow \lim_{x\rightarrow a}\left\left [ (f(x)-f(a)) \right(f^{2}(x)+f(x)f(a)+f^{2}(a)+1) ]=0 \lim_{x\rightarrow a}\left [ f^{3}(x) \right+f(x) -f^{3}(a)-f(a)]=0 \Rightarrow \lim_{x\rightarrow a}\left\left [ (f(x)-f(a)) \right(f^{2}(x)+f(x)f(a)+f^{2}(a)+1) ]=0](/forum/ext/geomar/texintegr/latexrender/pictures/77afc0f6b4707cb8ce0ce8470f82b870.png)
 θα είναι
θα είναι  . Άρα
. Άρα 
 είναι αύξουσα(είναι γνήσια αλλά δεν χρειάζεται)
είναι αύξουσα(είναι γνήσια αλλά δεν χρειάζεται) έχουμε
έχουμε
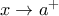 το κριτήριο παρεμβολής δίνει
το κριτήριο παρεμβολής δίνει

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες