Δίνονται οι παραγωγίσιμες συναρτήσεις
 με
με  και
και 
1) Nα βρεθούν οι τύποι των συναρτήσεων
2) Η εξίσωση της εφαπτομένης της
 στο σημείο
στο σημείο 
3) Το εμβαδό
 του χωρίου που περικλείεται απο την
του χωρίου που περικλείεται απο την  την ευθεία
την ευθεία  και τον άξονα
και τον άξονα 
4) Αν το σημείο
 απομακρύνεται απο τον άξονα
απομακρύνεται απο τον άξονα  με ταχύτητα
με ταχύτητα  μοναδες μήκους
μοναδες μήκους , να βρεθει ο ρυθμός μεταβολής του
, να βρεθει ο ρυθμός μεταβολής του  την χρονική στιγμή που η εφαπτομένη τέμνει τον
την χρονική στιγμή που η εφαπτομένη τέμνει τον  στο σημείο
στο σημείο 
5) Θεωρούμε την συνάρτηση
 . Δείξτε οτι υπάρχει μοναδικό
. Δείξτε οτι υπάρχει μοναδικό 

 .
. ΑΤΟΠΟ
ΑΤΟΠΟ είναι συνεχής στο
είναι συνεχής στο  ως παραγωγίσιμη, θα διατηρεί σταθερό πρόσημο σε αυτό.
ως παραγωγίσιμη, θα διατηρεί σταθερό πρόσημο σε αυτό. θα πρέπει
θα πρέπει 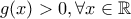
 παραγωγίσιμη στο
παραγωγίσιμη στο 



 .
. επαληθεύουν τις δοθείσες.
επαληθεύουν τις δοθείσες.
 και
και  ,
, ![\forall x \in \left[0,a \right] \forall x \in \left[0,a \right]](/forum/ext/geomar/texintegr/latexrender/pictures/acb22b09b5ca59f46fa8763f271ca7b2.png) άρα,
άρα, 

 .
.
 παραγωγίσιμη στο
παραγωγίσιμη στο  (μηδενίζεται μόνο για
(μηδενίζεται μόνο για 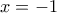 )
)

![\Delta _1 =\left(-\infty,0 \right] \Delta _1 =\left(-\infty,0 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/48a24d0f454f3af88f74676487de526c.png) και γνησίως αύξουσα στο
και γνησίως αύξουσα στο 
 εφόσον
εφόσον 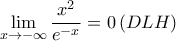


 και
και 
 επειδή
επειδή 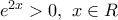 και
και  άρα
άρα  και
και  και επειδή από
και επειδή από  θα είναι
θα είναι  άρα ισχύει
άρα ισχύει  επομένως είναι
επομένως είναι  άρα
άρα  και αφού
και αφού  δηλαδή
δηλαδή 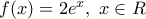 και τότε από
και τότε από 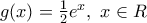 που εύκολα επαληθεύουν τις αρχικές ισότητες.
που εύκολα επαληθεύουν τις αρχικές ισότητες.

 ) και άρα
) και άρα ![E(\alpha )=2\left[ {{e}^{\alpha }}x-{{e}^{x}} \right]_{0}^{\alpha }=2(\alpha -1){{e}^{\alpha }}+2 E(\alpha )=2\left[ {{e}^{\alpha }}x-{{e}^{x}} \right]_{0}^{\alpha }=2(\alpha -1){{e}^{\alpha }}+2](/forum/ext/geomar/texintegr/latexrender/pictures/cbe83ca33a414238bc738d0eaf1ba5c5.png)
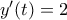 με
με  επομένως τότε
επομένως τότε  δηλαδή
δηλαδή  (1)
(1)  επομένως
επομένως  και λόγω (1)
και λόγω (1)  (2)
(2) τέμνει τον
τέμνει τον  στο
στο  και έτσι από (2)
και έτσι από (2) 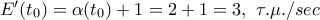
 παραγωγίσιμη με
παραγωγίσιμη με  άρα η
άρα η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο ![[0,\,\,1] [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/64486b1bb1fcabef4d7394f4c4b2a10d.png)
![h(0)\le h(x)\le h(1),\,\,\,x\in [0,\,\,1] h(0)\le h(x)\le h(1),\,\,\,x\in [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/369d7c8b637dfcaf27f6ffa71992ac74.png) και ολοκληρώνοντας έχουμε ότι
και ολοκληρώνοντας έχουμε ότι 
 το εμβαδον που σχηματίζουν
το εμβαδον που σχηματίζουν 
 το εμβαδον που σχηματίζουν
το εμβαδον που σχηματίζουν 
 το εμβαδον που σχηματίζουν
το εμβαδον που σχηματίζουν 





 , είναι :
, είναι : και
και 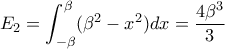
![\displaystyle{a=\sqrt[3]{9},~\beta=\sqrt[3]{18}} \displaystyle{a=\sqrt[3]{9},~\beta=\sqrt[3]{18}}](/forum/ext/geomar/texintegr/latexrender/pictures/9302ca18ba5e0f8719e3680c2c3e5a8a.png)
 .
.