 του
του  τετραγώνου
τετραγώνου  , παίρνουμε σημεία
, παίρνουμε σημεία  , ώστε :
, ώστε :  .
.Δείξτε ότι το τμήμα
 εφάπτεται του κύκλου
εφάπτεται του κύκλου  - έστω στο
- έστω στο  - και υπολογίστε το λόγο :
- και υπολογίστε το λόγο :  .
.Οι όροι συμμετοχής : Η πρώτη λύση Ευκλείδεια , η δεύτερη τριγωνομετρική και η τρίτη καρτεσιανή .
Στη συνέχεια "η πίστα είναι ελεύθερη" για κάθε είδους λύση ( διανυσματική , αναλυτική κ.λ.π.)

 φέρνω εφαπτομένη
φέρνω εφαπτομένη  στο τεταρτοκύκλιο. Τότε
στο τεταρτοκύκλιο. Τότε  . Προεκτείνω τη
. Προεκτείνω τη  στο
στο  .
.  στο τεταρτοκύκλιο.
στο τεταρτοκύκλιο. άρα
άρα  .
. .
. , άρα τα
, άρα τα  ταυτίζονται, όπως θέλαμε.
ταυτίζονται, όπως θέλαμε. Ορίζω το
Ορίζω το  Αρκεί να δείξω ότι
Αρκεί να δείξω ότι  και
και 
 και από Stewart στο
και από Stewart στο  , παίρνω
, παίρνω  και με αντίστροφο του
και με αντίστροφο του 
 , βρίσκω
, βρίσκω 

 από το
από το  .
. έχουμε διαδοχικά:
έχουμε διαδοχικά: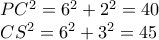

 οπότε
οπότε  άρα η
άρα η 
 , άρα η
, άρα η  .
. και
και 

 .
. αφού ως γνωστό
αφού ως γνωστό  .
. στα
στα  αντίστοιχα . Είναι
αντίστοιχα . Είναι 
 . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  έχω
έχω  . μετά τα πράγματα είναι πολύ απλά
. μετά τα πράγματα είναι πολύ απλά  και
και 
 εφάπτεται στις
εφάπτεται στις  και
και  ίσο με την
ίσο με την  θα είναι ο
θα είναι ο 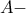 παρεγγεγραμμένος κύκλος του τριγώνου.
παρεγγεγραμμένος κύκλος του τριγώνου.
 είναι
είναι 
 άρα
άρα  .
. , άρα η
, άρα η  άρα
άρα  .
.

 .
.