Περιγραφική προσπάθεια..
i, ii) Τα όποια κοινά σημεία της γραφικής παράστασης της

με την αντιστροφή της θα βρίσκονται επί της διχοτόμου του πρώτου τεταρτημόριου. Οπότε για να τα βρούμε αρκεί να λύσουμε την εξίσωση

στο παραπάνω διάστημα. Θεωρούμε την συνάρτηση

στο διάστημα

. Παρατηρούμε ότι είναι περιττή, οπότε αρκεί να την μελετήσουμε για

. Στο διάστημα αυτό η συνάρτηση είναι συνεχής και παραγωγίσιμη με

Για

είναι

οπότε η

είναι γνησίως αύξουσα στο

. Άρα για κάθε

θα ισχύει

. Επομένως για

δεν υπάρχουν άλλα κοινά σημεία εκτός από το

.
Για

είναι

. (1)
Έστω ότι υπάρχει ένα

για το οποίο

. Τότε στο διάστημα
![[0,x_{0}] [0,x_{0}]](/forum/ext/geomar/texintegr/latexrender/pictures/f2227e7e0241f4841a3357fb19432306.png)
ισχύουν οι προυποθέσεις του θεωρήματος Rolle και άρα θα υπάρχει ένα

για το οποίο

. Πράγμα άτοπο λόγω της (1). Επομένως ούτε σε αυτή την περίπτωση υπάρχουν άλλα κοινά σημεία εκτός του

.
Για

η

(2).
Η συνάρτηση
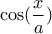
παίρνει θετικές (του διαστήματος
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)
) τιμές στο διάστημα

και μάλιστα λόγο της μονοτονίας της (γνησίως φθίνουσα ) θα έχει μοναδική ρίζα σε αυτό, έστω

. Για την οποία ισχύει

και

.
Στο διάστημα

η εξίσωση

δεν έχει λύσεις αφού είναι γνησίως φθίνουσα και

. Άρα θα είναι

. Στο διάστημα

η

είναι γνησίως αύξουσα και το όριό της καθώς τείνουμε στο δεξί άκρο του διαστήματος είναι συν άπειρο. Οπότε αρκούντος κοντά σε αυτό θα υπάρχει ένα

για το οποίο

. Στο διάστημα
![[x_{0}, x_{2}] [x_{0}, x_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/5fe7b7e27d76130803a5426fe81134fa.png)
ικανοποιούνται οι συνθήκες του θεωρήματος Bolzano, οπότε θα υπάρχει ένα

για το οποίο

. Το οποίο είναι και μοναδικό λόγω της μονοτονίας σε αυτό το διάστημα. Εύκολά βλέπουμε ότι εκτός του παρπαάνω διαστήματος δεν μπορεί να υπάρχει ρίζα της

.
Δείξαμε δηλαδή ότι υπάρχει μοναδική ρίζα για θετικά

. Ομοίως λόγω της περιττότητας της

υπάρχει μοναδική λύση για τα αρνητικά

και μαζί με την λύση στο μηδέν μας δίνουν ακριβώς τρία κοινά σημεία.
iii) Παρατηρούμε ότι για το σημείο

είναι

, για

. Άρα η ρίζα της

θα βρίσκεται στο διάστημα

. Όμως

.
Από την παραπάνω μελέτη της σχετικής θέσης του σημείου τομής των καμπυλών προκύπτει το σχήμα
[attachment=0]amepos_amergon.png[/attachment]
Επομένως το ζητούμενο εμβαδόν

, λόγω και των συμμετριών, θα δίνεται από το ολοκλήρωμα

(γνωστό ολοκλήρωμα, υπάρχει σε άσκηση του σχολικού βιβλίου).

 , κοίλη στο
, κοίλη στο ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) με
με  .
. για κάθε
για κάθε  , όπου
, όπου 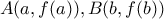
 , να δείξετε ότι
, να δείξετε ότι 
![f''(x)<0, x \in[a,b] f''(x)<0, x \in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/6075b416d9eb42ca67c62597bd8d934e.png) . Έστω
. Έστω ![t \in[a,b] t \in[a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/4bb81c7fd4a31b0b180a40951f89298f.png) και
και  το εμβαδό μεταξύ της
το εμβαδό μεταξύ της  , την εφαπτομένη της
, την εφαπτομένη της  και τις ευθείες
και τις ευθείες  . Να βρείτε την τιμή του
. Να βρείτε την τιμή του  για την οποία το
για την οποία το  που ορίζονται από τις σχέσεις
που ορίζονται από τις σχέσεις

 πραγματική μεταβλητή.
πραγματική μεταβλητή. και να την μελετήσετε ως προς την μονοτονία στα διάστηματα της μορφής
και να την μελετήσετε ως προς την μονοτονία στα διάστηματα της μορφής  .
. ώστε η εξίσωση
ώστε η εξίσωση  να έχει λύση σε διάστημα της μορφής
να έχει λύση σε διάστημα της μορφής  ,
,  .
. για τις οποίες η εξίσωση
για τις οποίες η εξίσωση 
 δύο ρίζες.Αν εφαρμόσουμε Rolle στο
δύο ρίζες.Αν εφαρμόσουμε Rolle στο ![[c,d] [c,d]](/forum/ext/geomar/texintegr/latexrender/pictures/c31d2b7df15fa7d119c2f8d13f69e10b.png) τότε υπάρχει
τότε υπάρχει  με
με 
 είναι γνησίως φθίνουσα.Αρα
είναι γνησίως φθίνουσα.Αρα 
![[v,b] [v,b]](/forum/ext/geomar/texintegr/latexrender/pictures/9080bd74c01b89225347b396dd00bf6d.png) .
. που είναι ΑΤΟΠΟ.
που είναι ΑΤΟΠΟ.![g(x)=f(b)\dfrac{x-a}{b-a}+f(a)\dfrac{x-b}{a-b},x\in [a,b] g(x)=f(b)\dfrac{x-a}{b-a}+f(a)\dfrac{x-b}{a-b},x\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/4ba61037cdb16a6993ba3cdd17757428.png)

 . Επίσης
. Επίσης  όπου
όπου  σταθερός αριθμός που εξαρτάται από τα
σταθερός αριθμός που εξαρτάται από τα 
 είναι γνησίως φθίνουσα.
είναι γνησίως φθίνουσα. σαν συνεχής θα έχει ολικό ελάχιστο σε ένα
σαν συνεχής θα έχει ολικό ελάχιστο σε ένα ![k\in [a,b] k\in [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/bf776abe5def3ca8691059d3b3076021.png)
 τότε
τότε  και
και 
 έχουμε ολικό μέγιστο.ΑΤΟΠΟ.
έχουμε ολικό μέγιστο.ΑΤΟΠΟ.  για
για 

 είναι
είναι 
 δίνει
δίνει  ενώ για
ενώ για  δίνει
δίνει  .
.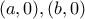 και τα σημεία που τέμνει η εφαπτομένη τις
και τα σημεία που τέμνει η εφαπτομένη τις 


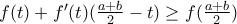
 με ισότητα αν
με ισότητα αν  είναι
είναι 

 , οι γραφικές παραστάσεις
, οι γραφικές παραστάσεις  και
και  της
της  , αντίστοιχα, έχουν περισσότερα από ένα σημεία τομής.
, αντίστοιχα, έχουν περισσότερα από ένα σημεία τομής. , να αποδειχθεί ότι οι
, να αποδειχθεί ότι οι  σημεία τομής.
σημεία τομής. , να βρεθεί το εμβαδόν του χωρίου που περικλείεται - αρχίζοντας από το
, να βρεθεί το εμβαδόν του χωρίου που περικλείεται - αρχίζοντας από το  , καταλίγοντας στο
, καταλίγοντας στο  , την ευθεία
, την ευθεία  και την
και την 
 στο παραπάνω διάστημα. Θεωρούμε την συνάρτηση
στο παραπάνω διάστημα. Θεωρούμε την συνάρτηση  στο διάστημα
στο διάστημα  . Παρατηρούμε ότι είναι περιττή, οπότε αρκεί να την μελετήσουμε για
. Παρατηρούμε ότι είναι περιττή, οπότε αρκεί να την μελετήσουμε για  . Στο διάστημα αυτό η συνάρτηση είναι συνεχής και παραγωγίσιμη με
. Στο διάστημα αυτό η συνάρτηση είναι συνεχής και παραγωγίσιμη με 
 είναι
είναι  οπότε η
οπότε η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  . Άρα για κάθε
. Άρα για κάθε  θα ισχύει
θα ισχύει  . Επομένως για
. Επομένως για  είναι
είναι  . (1)
. (1) για το οποίο
για το οποίο  . Τότε στο διάστημα
. Τότε στο διάστημα ![[0,x_{0}] [0,x_{0}]](/forum/ext/geomar/texintegr/latexrender/pictures/f2227e7e0241f4841a3357fb19432306.png) ισχύουν οι προυποθέσεις του θεωρήματος Rolle και άρα θα υπάρχει ένα
ισχύουν οι προυποθέσεις του θεωρήματος Rolle και άρα θα υπάρχει ένα  για το οποίο
για το οποίο  . Πράγμα άτοπο λόγω της (1). Επομένως ούτε σε αυτή την περίπτωση υπάρχουν άλλα κοινά σημεία εκτός του
. Πράγμα άτοπο λόγω της (1). Επομένως ούτε σε αυτή την περίπτωση υπάρχουν άλλα κοινά σημεία εκτός του  η
η  (2).
(2). 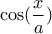 παίρνει θετικές (του διαστήματος
παίρνει θετικές (του διαστήματος ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) ) τιμές στο διάστημα
) τιμές στο διάστημα  και μάλιστα λόγο της μονοτονίας της (γνησίως φθίνουσα ) θα έχει μοναδική ρίζα σε αυτό, έστω
και μάλιστα λόγο της μονοτονίας της (γνησίως φθίνουσα ) θα έχει μοναδική ρίζα σε αυτό, έστω  . Για την οποία ισχύει
. Για την οποία ισχύει  και
και  .
.  η εξίσωση
η εξίσωση  δεν έχει λύσεις αφού είναι γνησίως φθίνουσα και
δεν έχει λύσεις αφού είναι γνησίως φθίνουσα και  . Άρα θα είναι
. Άρα θα είναι  . Στο διάστημα
. Στο διάστημα  η
η  για το οποίο
για το οποίο  . Στο διάστημα
. Στο διάστημα ![[x_{0}, x_{2}] [x_{0}, x_{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/5fe7b7e27d76130803a5426fe81134fa.png) ικανοποιούνται οι συνθήκες του θεωρήματος Bolzano, οπότε θα υπάρχει ένα
ικανοποιούνται οι συνθήκες του θεωρήματος Bolzano, οπότε θα υπάρχει ένα  για το οποίο
για το οποίο  . Το οποίο είναι και μοναδικό λόγω της μονοτονίας σε αυτό το διάστημα. Εύκολά βλέπουμε ότι εκτός του παρπαάνω διαστήματος δεν μπορεί να υπάρχει ρίζα της
. Το οποίο είναι και μοναδικό λόγω της μονοτονίας σε αυτό το διάστημα. Εύκολά βλέπουμε ότι εκτός του παρπαάνω διαστήματος δεν μπορεί να υπάρχει ρίζα της  .
.  είναι
είναι  , για
, για  . Άρα η ρίζα της
. Άρα η ρίζα της  θα βρίσκεται στο διάστημα
θα βρίσκεται στο διάστημα  . Όμως
. Όμως  .
.  , λόγω και των συμμετριών, θα δίνεται από το ολοκλήρωμα
, λόγω και των συμμετριών, θα δίνεται από το ολοκλήρωμα
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  για κάθε
για κάθε  . Επομένως είναι γνησίως αύξουσα, και επειδή είναι και συνεχής, έπεται ότι είναι 1-1; άρα αντιστρέψιμη.
. Επομένως είναι γνησίως αύξουσα, και επειδή είναι και συνεχής, έπεται ότι είναι 1-1; άρα αντιστρέψιμη. . Για να προσδιορισθούν αυτά τα σημεία αρκεί να βρεθούν τα σημεία τομής της
. Για να προσδιορισθούν αυτά τα σημεία αρκεί να βρεθούν τα σημεία τομής της  , για να υπάρχουν κι άλλα σημεία τομής πρέπει και αρκεί η
, για να υπάρχουν κι άλλα σημεία τομής πρέπει και αρκεί η  να βρίσκεται κάτω από την
να βρίσκεται κάτω από την 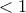 , δηλαδή
, δηλαδή 
 το σημείο τομής των
το σημείο τομής των  και η
και η  του χωρίου που περικλείεται από την
του χωρίου που περικλείεται από την ![\begin{aligned}
{\rm{E}}&=2\int_{0}^{\alpha}\big|x-f(x)\big|\,dx\\\noalign{\vspace{0.1cm}}
&=2\int_{0}^{\alpha}\big(x-{\varepsilon\varphi}\,\big(\tfrac{x}{\alpha}\big)\big)\,dx\\\noalign{\vspace{0.1cm}}
&=2\int_{0}^{\alpha}x\,dx-2\int_{0}^{\alpha}{\varepsilon\varphi}\,\big(\tfrac{x}{\alpha}\big)\,dx\\\noalign{\vspace{0.1cm}}
&\mathop{=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c}
{t\,=\,\tfrac{x}{\alpha}} \\\noalign{\vspace{0.05cm}}
{\alpha\, dt\,=\,dx} \\\noalign{\vspace{0.05cm}}
\end{subarray}}\,2\Big[\frac{x^2}{2}\Big]_{0}^{\alpha}-2\alpha\int_{0}^{1}{\varepsilon\varphi}\,{t}\,dt\\\noalign{\vspace{0.1cm}}
&=\alpha^2-2\alpha\int_{0}^{1}\frac{{\eta\mu}\,{t}}{{\sigma\upsilon\nu}\,{t}}\,dt\\\noalign{\vspace{0.1cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c}
{u\,=\,{\sigma\upsilon\nu}\,{t}} \\\noalign{\vspace{0.05cm}}
{-du\,=\,{\eta\mu}\,{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}\,\alpha^2+2\alpha\int_{{\sigma\upsilon\nu}\,{0}}^{{\sigma\upsilon\nu}\,{1}}\frac{1}{u}\,du\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\Big[\log|u|\Big]_{1}^{{\sigma\upsilon\nu}\,{1}}\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\log|{\sigma\upsilon\nu}\,{1}|\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\log({\sigma\upsilon\nu}\,{1})\,.\end{align*} \begin{aligned}
{\rm{E}}&=2\int_{0}^{\alpha}\big|x-f(x)\big|\,dx\\\noalign{\vspace{0.1cm}}
&=2\int_{0}^{\alpha}\big(x-{\varepsilon\varphi}\,\big(\tfrac{x}{\alpha}\big)\big)\,dx\\\noalign{\vspace{0.1cm}}
&=2\int_{0}^{\alpha}x\,dx-2\int_{0}^{\alpha}{\varepsilon\varphi}\,\big(\tfrac{x}{\alpha}\big)\,dx\\\noalign{\vspace{0.1cm}}
&\mathop{=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c}
{t\,=\,\tfrac{x}{\alpha}} \\\noalign{\vspace{0.05cm}}
{\alpha\, dt\,=\,dx} \\\noalign{\vspace{0.05cm}}
\end{subarray}}\,2\Big[\frac{x^2}{2}\Big]_{0}^{\alpha}-2\alpha\int_{0}^{1}{\varepsilon\varphi}\,{t}\,dt\\\noalign{\vspace{0.1cm}}
&=\alpha^2-2\alpha\int_{0}^{1}\frac{{\eta\mu}\,{t}}{{\sigma\upsilon\nu}\,{t}}\,dt\\\noalign{\vspace{0.1cm}}
&\mathop{=\!=\!=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c}
{u\,=\,{\sigma\upsilon\nu}\,{t}} \\\noalign{\vspace{0.05cm}}
{-du\,=\,{\eta\mu}\,{t}\,dt} \\\noalign{\vspace{0.05cm}}
\end{subarray}}\,\alpha^2+2\alpha\int_{{\sigma\upsilon\nu}\,{0}}^{{\sigma\upsilon\nu}\,{1}}\frac{1}{u}\,du\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\Big[\log|u|\Big]_{1}^{{\sigma\upsilon\nu}\,{1}}\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\log|{\sigma\upsilon\nu}\,{1}|\\\noalign{\vspace{0.1cm}}
&=\alpha^2+2\alpha\,\log({\sigma\upsilon\nu}\,{1})\,.\end{align*}](/forum/ext/geomar/texintegr/latexrender/pictures/b34dd524feac8b467b3706d79e5c0d77.png)
 .
. ,
,  .
. μηδενίζεται σε μεμονωμένα σημεία του πεδίου ορισμού της συμπεραίνουμε ότι η
μηδενίζεται σε μεμονωμένα σημεία του πεδίου ορισμού της συμπεραίνουμε ότι η  .
.![\displaystyle{\lim_{x\rightarrow -\infty } f(x) =\lim_{x\rightarrow -\infty } = \left [ x\left ( 1+\dfrac{1}{x} -\frac{sinx}{x}\right ) \right ] = -\infty \displaystyle{\lim_{x\rightarrow -\infty } f(x) =\lim_{x\rightarrow -\infty } = \left [ x\left ( 1+\dfrac{1}{x} -\frac{sinx}{x}\right ) \right ] = -\infty](/forum/ext/geomar/texintegr/latexrender/pictures/480fecca1788ac3a71b247f2f4b10adb.png) .
. .
. .
. .
.