![\underbrace{\frac{{\alpha_1+\alpha_2+...+\alpha_\nu}}{\nu}}_{\text{A}} \geq \underbrace{\sqrt[\nu]{\alpha_1\cdot\alpha_2\cdot...\cdot\alpha_\nu}}_{\text{G}} \underbrace{\frac{{\alpha_1+\alpha_2+...+\alpha_\nu}}{\nu}}_{\text{A}} \geq \underbrace{\sqrt[\nu]{\alpha_1\cdot\alpha_2\cdot...\cdot\alpha_\nu}}_{\text{G}}](/forum/ext/geomar/texintegr/latexrender/pictures/dc5041d126ceda4176adb9d433e0ed5a.png) , με
, με 
Έστω η συνάρτηση
 , με
, με  και
και  .
.α) Η
 έχει ολικό μέγιστο για
έχει ολικό μέγιστο για  , δηλαδή,
, δηλαδή,  ή
ή 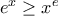 (1)
(1)β) Ονομάζω τον αριθμητικό μέσο των
 με
με  , και το γεωμετρικό μέσο με
, και το γεωμετρικό μέσο με  και θέτω στην (1):
και θέτω στην (1):



Πολλαπλασιάζω κατά μέλη και έχω:

Συντονιστής: spyros
![\underbrace{\frac{{\alpha_1+\alpha_2+...+\alpha_\nu}}{\nu}}_{\text{A}} \geq \underbrace{\sqrt[\nu]{\alpha_1\cdot\alpha_2\cdot...\cdot\alpha_\nu}}_{\text{G}} \underbrace{\frac{{\alpha_1+\alpha_2+...+\alpha_\nu}}{\nu}}_{\text{A}} \geq \underbrace{\sqrt[\nu]{\alpha_1\cdot\alpha_2\cdot...\cdot\alpha_\nu}}_{\text{G}}](/forum/ext/geomar/texintegr/latexrender/pictures/dc5041d126ceda4176adb9d433e0ed5a.png) , με
, με 
 , με
, με  και
και  .
. έχει ολικό μέγιστο για
έχει ολικό μέγιστο για  , δηλαδή,
, δηλαδή,  ή
ή 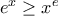 (1)
(1) με
με  , και το γεωμετρικό μέσο με
, και το γεωμετρικό μέσο με  και θέτω στην (1):
και θέτω στην (1):




Προς αποφυγήν παρεξηγήσεων ας προσθέσω ότι υπάρχουν δεκάδες και δεκάδες αποδείξεις της Cauchy οι περισσότερες από τις οποίες είναι ευκολότερες από την παραπάνω (ευρέως γνωστή, άλλωστε) απόδειξη.ΗρακληςΕυαγγελινος έγραψε:
, με
 αποδείξεις. Αν κάποιος έχει παραπομπή, ας μας την δώσει γιατί δυσκολεύομαι να ψάχνω στο ιντερνέτ.
αποδείξεις. Αν κάποιος έχει παραπομπή, ας μας την δώσει γιατί δυσκολεύομαι να ψάχνω στο ιντερνέτ. , να δείξετε ότι:
, να δείξετε ότι:![\forall \nu \in N: \frac{\alpha_1+\alpha_2+....+\alpha_\nu}{\nu} \geq \sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu} \forall \nu \in N: \frac{\alpha_1+\alpha_2+....+\alpha_\nu}{\nu} \geq \sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu}](/forum/ext/geomar/texintegr/latexrender/pictures/b2835a78df073d7b960641752f16efcc.png) (1)
(1)![\lambda=\sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu} \lambda=\sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu}](/forum/ext/geomar/texintegr/latexrender/pictures/42387a192c6d45b9d79d1a6012944244.png) , τότε:
, τότε: 

 , άρα:
, άρα: 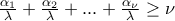 , από γνωστή ιδιότητα.
, από γνωστή ιδιότητα. , δηλαδη:
, δηλαδη: ![\frac{\alpha_1+\alpha_2+....+\alpha_\nu}{\nu} \geq \sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu} \frac{\alpha_1+\alpha_2+....+\alpha_\nu}{\nu} \geq \sqrt[\nu]{\alpha_1\alpha_2...\alpha_\nu}](/forum/ext/geomar/texintegr/latexrender/pictures/c15b15a9d61d2b2964d238431a730c4c.png) .
. , δηλαδή όταν:
, δηλαδή όταν:  .
. και
και  , με
, με  και ζητείται να κατασκευαστούν τα ευθύγραμμα τμήματα
και ζητείται να κατασκευαστούν τα ευθύγραμμα τμήματα 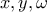 , ώστε:
, ώστε: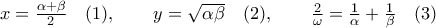 .
. και
και  . Με διάμετρο το τμήμα
. Με διάμετρο το τμήμα  γράφουμε κύκλο κέντρου
γράφουμε κύκλο κέντρου  . Φέρνουμε την εφαπτομένη
. Φέρνουμε την εφαπτομένη  και την κάθετη
και την κάθετη  επί την
επί την  . Τέλος, φέρνουμε και το τμήμα
. Τέλος, φέρνουμε και το τμήμα  .
. , και έτσι:
, και έτσι:  .
. . Άρα
. Άρα  .
. , και έτσι:
, και έτσι:  .
. . Άρα
. Άρα  .
. ή
ή 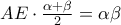 , και έτσι:
, και έτσι:  ή
ή  .
.  , και έτσι:
, και έτσι:  ή
ή  .
. , και έτσι
, και έτσι  .
. , όπου
, όπου  υποτείνουσα του ορθογωνίου τριγώνου
υποτείνουσα του ορθογωνίου τριγώνου  και
και  υποτείνουσα του ορθογωνίου τριγώνου
υποτείνουσα του ορθογωνίου τριγώνου  , ή
, ή  .
.Aπάντηση στον κ. Μ. Λάμπρου (Σχετικά με τις παρεμβάσεις του στις αναρτήσεις μου της 18ης Νοεμβρίου 2016)Mihalis_Lambrou έγραψε:Προσοχή στα τυπογραφικά σφάλματα εδώ:
Προς αποφυγήν παρεξηγήσεων ας προσθέσω ότι υπάρχουν δεκάδες και δεκάδες αποδείξεις της Cauchy οι περισσότερες από τις οποίες είναι ευκολότερες από την παραπάνω (ευρέως γνωστή, άλλωστε) απόδειξη.ΗρακληςΕυαγγελινος έγραψε:
, με
Νομίζω κάποιο βιβλίο ή άρθρο έχει μαζέψει πάνω απόαποδείξεις. Αν κάποιος έχει παραπομπή, ας μας την δώσει γιατί δυσκολεύομαι να ψάχνω στο ιντερνέτ.
 , και
, και  τότε το άθροισμα αυτών
τότε το άθροισμα αυτών 
 ισχύει ως ισότητα
ισχύει ως ισότητα και πρέπει
και πρέπει  , που αληθεύει.
, που αληθεύει.
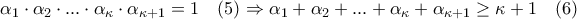
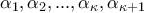 δεν είναι ανά δύο ίσοι, τότε μεταξύ αυτών υπάρχει ένας τουλάχιστο μικρότερος του 1, έστω
δεν είναι ανά δύο ίσοι, τότε μεταξύ αυτών υπάρχει ένας τουλάχιστο μικρότερος του 1, έστω  και ένας τουλάχιστο μεγαλύτερος του 1, έστω
και ένας τουλάχιστο μεγαλύτερος του 1, έστω  .
. , και η (5) γράφεται
, και η (5) γράφεται  , δηλαδή γινόμενο
, δηλαδή γινόμενο  παραγόντων, οπότε το άθροισμα αυτών
παραγόντων, οπότε το άθροισμα αυτών  , η οποία βάσει της (7) γίνεται:
, η οποία βάσει της (7) γίνεται: 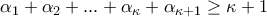 , που είναι η ζητούμενη (6).
, που είναι η ζητούμενη (6).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης