Σελίδα 31 από 37
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Κυρ Φεβ 21, 2016 9:39 pm
από vittasko
KARKAR έγραψε:Άσκηση 211
Στο άκρο

της διαγωνίου

, ορθογωνίου

, φέρω κάθετη , η οποία τέμνει τις προεκτάσεις των

στα σημεία
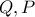
αντίστοιχα . Ονομάζω

το μέσο του

, παίρνω τυχαίο σημείο

της

και γράφω τους κύκλους ,
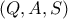
,

, οι οποίοι τέμνουν τις προεκτάσεις των

στα

αντίστοιχα . Δείξτε ότι οι ευθείες

τέμνονται σε σημείο - το οποίο ονομάζω

- της

.
Έστω

, οι περίκυκλοι των τριγώνων

αντιστοίχως και ας είναι

και

.
Έστω τα σημεία

και αρκεί να αποδειχθεί ότι

, γιατί η ευθεία που συνδέει το σημείο τομής των διαγωνίων τραπεζίου με το σημείο τομής των ευθειών των μη παραλλήλων πλευρών του, περνάει από τα μέσα των βάσεών του ( γνωστό αποτέλεσμα ).

Από το εγγράψιμο τετράπλευρο

έχουμε

Από

και

, λόγω του ορθογωνίου τριγώνου
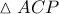
με

,
προκύπτει


και ομοίως αποδεικνύεται ότι

Από το τραπέζιο

τώρα, έχουμε

Από το ορθογώνιο παραλληλόγραμμο

έχουμε
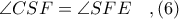
Από


και άρα, τα σημεία

είναι συνευθειακά.
Ομοίως αποδεικνύεται ότι και τα σημεία

είναι συνευθειακά και επομένως, και τα τέσσερα σημεία

ανήκουν στην ίδια ευθεία.

- Συλλογή ασκήσεων με ορθοπγώνια - Άσκηση 211.
- f=40_t=52292_211.PNG (28.34 KiB) Προβλήθηκε 1639 φορές

Από

και
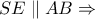



Αλλά, από


και από


Από


Από


και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 2:04 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 6:21 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε:Άσκηση 211
Το συνημμένο Άσκηση 210.png δεν είναι πλέον διαθέσιμο
Στο άκρο

της διαγωνίου

, ορθογωνίου

, φέρω κάθετη , η οποία τέμνει
τις προεκτάσεις των

στα σημεία
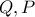
αντίστοιχα . Ονομάζω

το μέσο
του

, παίρνω τυχαίο σημείο

της

και γράφω τους κύκλους ,
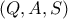
,

, οι οποίοι τέμνουν τις προεκτάσεις των

στα

αντίστοιχα .
Δείξτε ότι οι ευθείες

τέμνονται σε σημείο - το οποίο ονομάζω

- της

.
Καλησπέρα....
Έστω
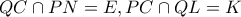
Είναι


και
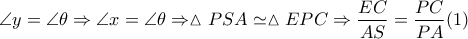

είναι ισοσκελές τραπέζιο


και

μέσον της

(αφού

)
Από θ.κεντρικής δέσμης προκύπτει το ζητούμενο

- a211.png (53.95 KiB) Προβλήθηκε 1609 φορές
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 6:56 pm
από vittasko
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 8:58 pm
από KARKAR
Άσκηση 213

- Άσκηση 212.png (11.36 KiB) Προβλήθηκε 1559 φορές
Σε τυχαίο σημείο

της πλευράς

ορθογωνίου

, υψώνουμε κάθετη ,
η οποία τέμνει την

στο

και τον περίκυκλο στο

. Η παράλληλη από το

προς τη

τέμνει τις προεκτάσεις των

στα

. Δείξτε ότι

Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 9:40 pm
από sakis1963
KARKAR έγραψε:Άσκηση 213
Το συνημμένο Άσκηση 212.png δεν είναι πλέον διαθέσιμο
Σε τυχαίο σημείο

της πλευράς

ορθογωνίου

, υψώνουμε κάθετη ,
η οποία τέμνει την

στο

και τον περίκυκλο στο

. Η παράλληλη από το

προς τη

τέμνει τις προεκτάσεις των

στα

. Δείξτε ότι

Άσκηση 213

- 213.png (21.91 KiB) Προβλήθηκε 1543 φορές
Καλησπέρα.
Από δύναμη σημείου

έχουμε

...(1)
Κλίση του

είναι
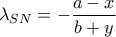
και του

είναι

άρα λόγω της (1)

άρα

Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 10:09 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
KARKAR έγραψε:Άσκηση 213
Σε τυχαίο σημείο

της πλευράς

ορθογωνίου

, υψώνουμε κάθετη , η οποία τέμνει την

στο

και τον περίκυκλο στο

. Η παράλληλη από το

προς τη

τέμνει τις προεκτάσεις των

στα

. Δείξτε ότι


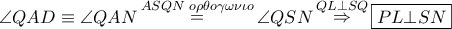 Στάθης
Στάθης
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 10:10 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε:Άσκηση 213
Το συνημμένο Άσκηση 212.png δεν είναι πλέον διαθέσιμο
Σε τυχαίο σημείο

της πλευράς

ορθογωνίου

, υψώνουμε κάθετη ,
η οποία τέμνει την

στο

και τον περίκυκλο στο

. Η παράλληλη από το

προς τη

τέμνει τις προεκτάσεις των

στα

. Δείξτε ότι


ισοσκελές τραπέζιο

και

εγγράψιμο

Κάπου την έχω ξαναδεί...

- a213.png (17.51 KiB) Προβλήθηκε 1540 φορές
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Δευ Φεβ 22, 2016 10:36 pm
από sakis1963
Μιχάλης Τσουρακάκης έγραψε:KARKAR έγραψε:Άσκηση 213
Άσκηση 212.png
Κάπου την έχω ξαναδεί...
Δίκιο έχεις Μιχάλη, είναι η
Ασκηση 189
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Τρί Φεβ 23, 2016 4:49 pm
από Doloros
Άσκηση 214

- Ορθογώνια_KARKAR_214.png (8.53 KiB) Προβλήθηκε 1465 φορές
Έστω ορθογώνιο

και τα σημεία

των πλευρών του

αντίστοιχα , τέτοια ώστε το τρίγωνο

να είναι ισόπλευρο.
Δείξετε ότι

.
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Τρί Φεβ 23, 2016 8:23 pm
από KARKAR
Doloros έγραψε:Άσκηση 214
Έστω ορθογώνιο

και τα σημεία

των πλευρών του

αντίστοιχα ,
τέτοια ώστε το τρίγωνο

να είναι ισόπλευρο . Δείξετε ότι

.
Σπεύδω να παραπέμψω στην εκπληκτική λύση Βαρβεράκη
εδώ
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Τρί Φεβ 23, 2016 10:00 pm
από sakis1963
Doloros έγραψε:Άσκηση 214
Ορθογώνια_KARKAR_214.png
Έστω ορθογώνιο

και τα σημεία

των πλευρών του

αντίστοιχα , τέτοια ώστε το τρίγωνο

να είναι ισόπλευρο.
Δείξετε ότι

.
Καλησπέρα, και
εδώ
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Τετ Φεβ 24, 2016 8:19 pm
από KARKAR
Άσκηση 215

- Άσκηση 213.png (17.58 KiB) Προβλήθηκε 1382 φορές
Οι κορυφές

του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε
το εμβαδόν του

. Αν η έλλειψη έχει εξίσωση

, για ποια σχέση των
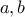
, εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος

;
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Τετ Φεβ 24, 2016 9:13 pm
από ealexiou
KARKAR έγραψε:Άσκηση 215
Το συνημμένο Άσκηση 213.png δεν είναι πλέον διαθέσιμο
Οι κορυφές

του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε
το εμβαδόν του

. Αν η έλλειψη έχει εξίσωση

, για ποια σχέση των
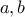
, εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος

;

- Συλλογή ασκήσεων με ορθογώνια Ασκ. 215.png (27.82 KiB) Προβλήθηκε 1373 φορές
Για εξίσωση της έλλειψης
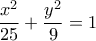
Αν

και

τότε

άρα

Για εξίσωση της έλλειψης

Για να εγγραφεί το ορθογώνιο πρέπει


(στην ισότητα προκύπτει τετράγωνο)
Αν

και

τότε

Άρα

Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Πέμ Φεβ 25, 2016 11:38 am
από KARKAR
Άσκηση 216

- Άσκηση 216.png (10.23 KiB) Προβλήθηκε 1319 φορές
Δύο κύκλοι , οι οποίοι διέρχονται ο καθένας από δύο απέναντι κορυφές ορθογωνίου

,
τέμνονται στα σημεία

και

. Δείξτε ότι το

διέρχεται από το κέντρο

του ορθογωνίου .
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Πέμ Φεβ 25, 2016 5:32 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε:Άσκηση 216
Το συνημμένο Άσκηση 216.png δεν είναι πλέον διαθέσιμο
Δύο κύκλοι , οι οποίοι διέρχονται ο καθένας από δύο απέναντι κορυφές ορθογωνίου

,
τέμνονται στα σημεία

και

. Δείξτε ότι το

διέρχεται από το κέντρο

του ορθογωνίου .
Με

περίκυκλο του

οι ριζικοί άξονες των
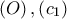
και

είναι

αντίστοιχα, που τέμνονται στο

.
Επομένως το

έχει ίδια δύναμη ως προς τους τρεις κύκλους ,άρα θα ανήκει και στο ριζικό άξονα των

που είναι ο


- a216.png (20.71 KiB) Προβλήθηκε 1301 φορές
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Κυρ Φεβ 28, 2016 8:56 am
από KARKAR
Άσκηση 217

- Άσκηση 216.png (15.02 KiB) Προβλήθηκε 1257 φορές
Η πλευρά

ορθογωνίου

που είναι εγγεγραμμένο σε κύκλο , είναι παράλληλη
προς τη διάμετρο

. Σχεδιάζω το ( επίσης ) ορθογώνιο

. Πώς πρέπει να επιλεγεί
η κορυφή

, ώστε ο λόγος

, να ισούται με

;
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Κυρ Φεβ 28, 2016 9:50 am
από george visvikis
KARKAR έγραψε:Άσκηση 217
Το συνημμένο Άσκηση 216.png δεν είναι πλέον διαθέσιμο
Η πλευρά

ορθογωνίου

που είναι εγγεγραμμένο σε κύκλο , είναι παράλληλη
προς τη διάμετρο

. Σχεδιάζω το ( επίσης ) ορθογώνιο

. Πώς πρέπει να επιλεγεί
η κορυφή

, ώστε ο λόγος

, να ισούται με

;
Καλημέρα Θανάση, καλημέρα σε όλους.
Έστω


- 217.png (16.39 KiB) Προβλήθηκε 1248 φορές

, απ' όπου προσδιορίζεται η κορυφή

.
Παίρνω πάνω στην

τμήμα ίσο με

και φέρνω κάθετη στην

που τέμνει τον κύκλο στα

, κλπ.
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Κυρ Φεβ 28, 2016 11:56 am
από george visvikis
Άσκηση 218

- 218.png (11.87 KiB) Προβλήθηκε 1229 φορές
Κύκλος κέντρου

διέρχεται από τις κορυφές

ορθογωνίου

. Να βρεθεί συναρτήσει των διαστάσεων

του
ορθογωνίου η ελάχιστη απόσταση του

από μία κορυφή του ορθογωνίου. (Το σχήμα είναι ενδεικτικό, αλλά όχι δεσμευτικό).
Re: Συλλογή ασκήσεων με ορθογώνια
Δημοσιεύτηκε: Κυρ Φεβ 28, 2016 3:14 pm
από ealexiou
george visvikis έγραψε:Άσκηση 218
Κύκλος κέντρου

διέρχεται από τις κορυφές

ορθογωνίου

. Να βρεθεί συναρτήσει των διαστάσεων

του ορθογωνίου η ελάχιστη απόσταση του

από μία κορυφή του ορθογωνίου. (Το σχήμα είναι ενδεικτικό, αλλά όχι δεσμευτικό).
Γεια σου Γιώργο

- Συλλογή ασκήσεων με ορθογώνια Ασκ. 218.png (20.43 KiB) Προβλήθηκε 1219 φορές
Είχα γράψει αρχικά "Δεν είμαι και σίγουρος ότι έχω αντιληφθεί σωστά το ζητούμενο".
Τώρα είμαι σίγουρος μετά την επιβεβαίωση (της ορθότητας του σχήματος) - καλύτερη δεν γίνεται

- από τον θεματοθέτη, οπότε αναρτώ και τους υπολογισμούς και αίρω την απόκρυψη.
Προφανώς το κέντρο του κύκλου βρίσκεται πάνω στην μεσοκάθετο στο

, άρα η ελάχιστη απόσταση θα είναι είτε από την κορυφή

στη θέση

(

) είτε από την κορυφή

σε σημείο
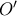
, συμμετρικό του

ως προς

.
Το ορθογώνιο

είναι, προφανώς, εγγράψιμο οπότε


, (

ακτίνα του πράσινου κύκλου).
Όμως

, οπότε:


Είναι




της διαγωνίου
, ορθογωνίου
, φέρω κάθετη , η οποία τέμνει τις προεκτάσεις των
στα σημεία
αντίστοιχα . Ονομάζω
το μέσο του
, παίρνω τυχαίο σημείο
της
και γράφω τους κύκλους ,
,
, οι οποίοι τέμνουν τις προεκτάσεις των
στα
αντίστοιχα . Δείξτε ότι οι ευθείες
τέμνονται σε σημείο - το οποίο ονομάζω
- της
.
 , οι περίκυκλοι των τριγώνων
, οι περίκυκλοι των τριγώνων  αντιστοίχως και ας είναι
αντιστοίχως και ας είναι  και
και  .
. και αρκεί να αποδειχθεί ότι
και αρκεί να αποδειχθεί ότι  , γιατί η ευθεία που συνδέει το σημείο τομής των διαγωνίων τραπεζίου με το σημείο τομής των ευθειών των μη παραλλήλων πλευρών του, περνάει από τα μέσα των βάσεών του ( γνωστό αποτέλεσμα ).
, γιατί η ευθεία που συνδέει το σημείο τομής των διαγωνίων τραπεζίου με το σημείο τομής των ευθειών των μη παραλλήλων πλευρών του, περνάει από τα μέσα των βάσεών του ( γνωστό αποτέλεσμα ). Από το εγγράψιμο τετράπλευρο
Από το εγγράψιμο τετράπλευρο  έχουμε
έχουμε 
 και
και  , λόγω του ορθογωνίου τριγώνου
, λόγω του ορθογωνίου τριγώνου 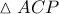 με
με  ,
, 
 και ομοίως αποδεικνύεται ότι
και ομοίως αποδεικνύεται ότι 
 τώρα, έχουμε
τώρα, έχουμε 
 έχουμε
έχουμε 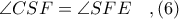

 και άρα, τα σημεία
και άρα, τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. είναι συνευθειακά και επομένως, και τα τέσσερα σημεία
είναι συνευθειακά και επομένως, και τα τέσσερα σημεία  ανήκουν στην ίδια ευθεία.
ανήκουν στην ίδια ευθεία.
 Από
Από  και
και 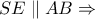




 και από
και από 




 και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
και το ισοδύναμο ζητούμενο έχει αποδειχθεί.
 και με
και με  προκύπτει ότι τα τρίγωνα
προκύπτει ότι τα τρίγωνα  είναι
είναι  είναι ο ορθοπόλος του
είναι ο ορθοπόλος του  .
.



 και με όμοιο τρόπο προκύπτει ότι
και με όμοιο τρόπο προκύπτει ότι  .
.
 .
.
 ομοκυκλικά και με
ομοκυκλικά και με  σύμφωνα με το
σύμφωνα με το το οποίο είναι το μέσο της
το οποίο είναι το μέσο της  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.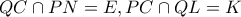

 και
και 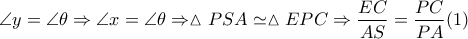
 είναι ισοσκελές τραπέζιο
είναι ισοσκελές τραπέζιο 
 και
και  μέσον της
μέσον της  (αφού
(αφού  )
)
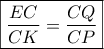
 ορθογωνίου
ορθογωνίου  στο
στο  και τον περίκυκλο στο
και τον περίκυκλο στο  . Η παράλληλη από το
. Η παράλληλη από το  στα
στα 
 έχουμε
έχουμε  ...(1)
...(1) είναι
είναι 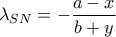 και του
και του  είναι
είναι  άρα λόγω της (1)
άρα λόγω της (1)

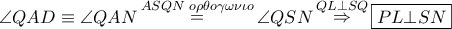
 ισοσκελές τραπέζιο
ισοσκελές τραπέζιο 
 εγγράψιμο
εγγράψιμο
 των πλευρών του
των πλευρών του  αντίστοιχα , τέτοια ώστε το τρίγωνο
αντίστοιχα , τέτοια ώστε το τρίγωνο  να είναι ισόπλευρο.
να είναι ισόπλευρο. .
. του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε
του ορθογωνίου του σχήματος είναι οι εστίες της έλλειψης . Υπολογίστε , για ποια σχέση των
, για ποια σχέση των 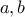 , εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος
, εξασφαλίζεται η ύπαρξη αυτού του ορθογωνίου και ποιος είναι τότε ο λόγος  ;
;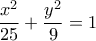
 και
και  τότε
τότε 


 (στην ισότητα προκύπτει τετράγωνο)
(στην ισότητα προκύπτει τετράγωνο)

 διέρχεται από το κέντρο
διέρχεται από το κέντρο  του ορθογωνίου .
του ορθογωνίου . περίκυκλο του
περίκυκλο του  οι ριζικοί άξονες των
οι ριζικοί άξονες των  και
και  είναι
είναι  αντίστοιχα, που τέμνονται στο
αντίστοιχα, που τέμνονται στο  .
. που είναι ο
που είναι ο 
 . Σχεδιάζω το ( επίσης ) ορθογώνιο
. Σχεδιάζω το ( επίσης ) ορθογώνιο  . Πώς πρέπει να επιλεγεί
. Πώς πρέπει να επιλεγεί , να ισούται με
, να ισούται με  ;
;
 , απ' όπου προσδιορίζεται η κορυφή
, απ' όπου προσδιορίζεται η κορυφή  και φέρνω κάθετη στην
και φέρνω κάθετη στην  , κλπ.
, κλπ. ορθογωνίου
ορθογωνίου  του
του  , άρα η ελάχιστη απόσταση θα είναι είτε από την κορυφή
, άρα η ελάχιστη απόσταση θα είναι είτε από την κορυφή  ) είτε από την κορυφή
) είτε από την κορυφή  σε σημείο
σε σημείο  , συμμετρικό του
, συμμετρικό του 
 , (
, ( ακτίνα του πράσινου κύκλου).
ακτίνα του πράσινου κύκλου).  , οπότε:
, οπότε:




