 είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  αντίστοιχα , ορθογωνίου
αντίστοιχα , ορθογωνίου  ,
, διαστάσεων
 . Η διαδρομή
. Η διαδρομή  είναι συντομότερη ή η
είναι συντομότερη ή η  ;
;Συντονιστής: Γιώργος Ρίζος
 είναι τα μέσα των πλευρών
είναι τα μέσα των πλευρών  αντίστοιχα , ορθογωνίου
αντίστοιχα , ορθογωνίου  ,
,  . Η διαδρομή
. Η διαδρομή  είναι συντομότερη ή η
είναι συντομότερη ή η  ;
; και
και  , άρα
, άρα  (1)
(1) και
και  , άρα
, άρα  (2)
(2) 

 , όπου
, όπου  θετικός πραγματικός.
θετικός πραγματικός.




 , που ισχύει από την ανισότητα
, που ισχύει από την ανισότητα  .
.Καλημέρα!KARKAR έγραψε:Μικρότερη διαδρομή.pngΤα σημείαείναι τα μέσα των πλευρών
αντίστοιχα , ορθογωνίου
,
διαστάσεων. Η διαδρομή
είναι συντομότερη ή η
;





 είναι εσωτερικό σημείο τριγώνου
είναι εσωτερικό σημείο τριγώνου  , τότε
, τότε  .
. το μέσο της
το μέσο της  , και
, και  το
το ως προς την ευθεία
ως προς την ευθεία 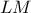 , τότε προφανώς
, τότε προφανώς  .
. , του
, του  , ως προς την
, ως προς την  είναι σημείο του
είναι σημείο του 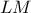 ( γιατί; ) , συνεπώς
( γιατί; ) , συνεπώς 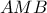 , δηλαδή :
, δηλαδή :  , ό. έ . δ.
, ό. έ . δ. , με ύψωση στο τετράγωνο
, με ύψωση στο τετράγωνο  , με δεύτερη ύψωση φθάνει στην
, με δεύτερη ύψωση φθάνει στην  , ενώ με μια τρίτη ύψωση , καταλήγει στην
, ενώ με μια τρίτη ύψωση , καταλήγει στην  ,
,Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες