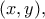 για τα οποία ισχύει
για τα οποία ισχύει
Συντονιστής: chris_gatos
Σου στέλνω με Π.Μ. την τελική απάντηση (για να μην την χαλάσω από τους υπόλοιπους που ενδεχομένως να θέλουν να την προσπαθήσουν: Εσύ με την σειρά σου, αν θέλεις διαβάζεις το Π.Μ.). Γνωρίζοντας την τελική απάντηση, είναι αρκετά ευκολότερο να βρεις απόδειξη. Θε περιμένω λίγο πριν γράψω λύση, αν και είμαι βέβαιος ότι δεν θα χρειαστεί.Eukleidis έγραψε:Αν γίνεται να δούμε μια λύση γι αυτή γιατί με έχει παιδέψει αρκετά και δε βλέπω κάποιο δρόμο
Ξεχάστηκε.matha έγραψε:Να παραστήσετε γραφικά τα σημείαγια τα οποία ισχύει
 εύκολα βλέπουμε ότι τα σημεία της ευθείας
εύκολα βλέπουμε ότι τα σημεία της ευθείας  ικανοποιούν την δοθείσα εξίσωση. Θα δείξουμε ότι δεν υπάρχουν άλλα σημεία στο γράφημα.
ικανοποιούν την δοθείσα εξίσωση. Θα δείξουμε ότι δεν υπάρχουν άλλα σημεία στο γράφημα. (όμοια αν
(όμοια αν  ) τότε η αρχική δίνει
) τότε η αρχική δίνει  που σημαίνει ότι το μόνο σημείο στους άξονες είναι το
που σημαίνει ότι το μόνο σημείο στους άξονες είναι το  . Οπότε μπορούμε από 'δω και πέρα να υποθέσουμε ότι
. Οπότε μπορούμε από 'δω και πέρα να υποθέσουμε ότι 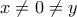 .
. 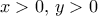 τότε
τότε  , ισοδύναμα
, ισοδύναμα  , άτοπο.
, άτοπο. βρίσκεται στο γράφημα τότε (απλό) και το
βρίσκεται στο γράφημα τότε (απλό) και το  βρίσκεται στο γράφημα. Άρα, από το 1), δεν υπάρχουν σημεία στο τρίτο τεταρτημόριο. Επίσης αρκεί να βρούμε τα σημεία στο δεύτερο τεταρτημόριο γιατί αυτόματα θα προσδιορίσουμε και του τέταρτου.
βρίσκεται στο γράφημα. Άρα, από το 1), δεν υπάρχουν σημεία στο τρίτο τεταρτημόριο. Επίσης αρκεί να βρούμε τα σημεία στο δεύτερο τεταρτημόριο γιατί αυτόματα θα προσδιορίσουμε και του τέταρτου. . Για ευκολία (αν και δεν είναι απαραίτητο) κάνουμε την αλλαγή μεταβλητής
. Για ευκολία (αν και δεν είναι απαραίτητο) κάνουμε την αλλαγή μεταβλητής 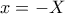 οπότε τώρα
οπότε τώρα  και η δοθείσα γίνεται
και η δοθείσα γίνεται  .
. είναι τα
είναι τα  και μόνον αυτά.
και μόνον αυτά.  ανήκει στο γράφημα της
ανήκει στο γράφημα της  τότε και το
τότε και το 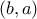 είναι στο ίδιο γράφημα οπότε μπορούμε χωρίς βλάβη να υποθέσουμε ότι ισχύει
είναι στο ίδιο γράφημα οπότε μπορούμε χωρίς βλάβη να υποθέσουμε ότι ισχύει 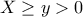 . Θα δείξουμε ότι η
. Θα δείξουμε ότι η  οδηγεί σε άτοπο, οπότε μένει η ζητούμενη
οδηγεί σε άτοπο, οπότε μένει η ζητούμενη  .
. σταθερό, εξετάζουμε την συνάρτηση
σταθερό, εξετάζουμε την συνάρτηση 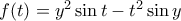 στο
στο ![[y, X] [y, X]](/forum/ext/geomar/texintegr/latexrender/pictures/b53549ad4a0fe05f68d42fc83b3dfa46.png) . Από Rolle υπάρχει
. Από Rolle υπάρχει ![\xi \in [y, X] \xi \in [y, X]](/forum/ext/geomar/texintegr/latexrender/pictures/4e3edd725c97ca70aca326c3e7d23b02.png) με
με 
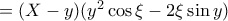
 τώρα γράφεται
τώρα γράφεται 
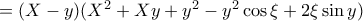
![=(X-y)\left [ X(X-y) + y^2(1-\cos \xi) + 2Xy + 2\xi \sin y \right ] =(X-y)\left [ X(X-y) + y^2(1-\cos \xi) + 2Xy + 2\xi \sin y \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/6151477dc153e835e0b6e685b38bd2e5.png)
![\ge (X-y)\left [ \underbrace {X(X-y)}_ {> 0} + \underbrace {y^2(1-\cos \xi)}_{\ge 0} + \underbrace {2\xi (y + \sin y)}_{\ge 0} \right ] >0 \ge (X-y)\left [ \underbrace {X(X-y)}_ {> 0} + \underbrace {y^2(1-\cos \xi)}_{\ge 0} + \underbrace {2\xi (y + \sin y)}_{\ge 0} \right ] >0](/forum/ext/geomar/texintegr/latexrender/pictures/601e66ce25b6e6116ec1e740d470f819.png) , άτοπο.
, άτοπο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες