 φέρουμε τις εφαπτόμενες προς τον κύκλο με εξίσωση :
φέρουμε τις εφαπτόμενες προς τον κύκλο με εξίσωση : 
ημιευθείες
 . Σε σημείο
. Σε σημείο  του κύκλου φέρουμε τρίτη εφαπτομένη , η οποία τέμνει τις
του κύκλου φέρουμε τρίτη εφαπτομένη , η οποία τέμνει τιςπροηγούμενες στα σημεία
 . Ποια είναι η τετμημένη του σημείου
. Ποια είναι η τετμημένη του σημείου  , αν :
, αν :  ;
;* Ενδιαφερόμαστε μόνο για την περίπτωση που το
 ανήκει στο μείζον τόξο
ανήκει στο μείζον τόξο  .
.
 οι προβολές των
οι προβολές των  στον άξονα
στον άξονα  Θέτω
Θέτω  άρα
άρα 
 οπότε,
οπότε,  και
και  Αν
Αν  τότε:
τότε:

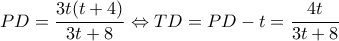 και
και 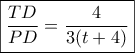
 κι επειδή
κι επειδή  το
το  είναι αριστερά του
είναι αριστερά του  άρα
άρα 