 , τέμνει τους
, τέμνει τουςθετικούς ημιάξονες
 στα σημεία
στα σημεία  αντίστοιχα και έστω
αντίστοιχα και έστω  .
.α) Υπολογίστε την ( σταθερή ! ) τιμή της παράστασης :
 .
.β) Δείξτε ότι το ελάχιστο εμβαδόν του
 , ισούται με
, ισούται με  .
.Συντονιστής: Τηλέγραφος Κώστας
 , τέμνει τους
, τέμνει τους στα σημεία
στα σημεία  αντίστοιχα και έστω
αντίστοιχα και έστω  .
. .
. , ισούται με
, ισούται με  .
. . Η εξίσωση της ευθείας, αφού διέρχεται από το σταθερό σημείο
. Η εξίσωση της ευθείας, αφού διέρχεται από το σταθερό σημείο  , είναι:
, είναι:  . Το σημείο
. Το σημείο  έχει τεταγμένη
έχει τεταγμένη  , οπότε:
, οπότε:  . Το σημείο
. Το σημείο  έχει τετμημένη
έχει τετμημένη  , οπότε
, οπότε 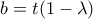 .
.

 έχει εμβαδόν:
έχει εμβαδόν: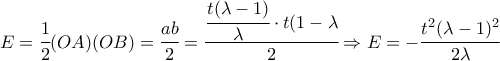
 . Η εξίσωση (ως προς
. Η εξίσωση (ως προς 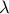 ) αυτή πρέπει να έχει πραγματικές ρίζες, οπότε για τη διακρίνουσα της θα ισχύει:
) αυτή πρέπει να έχει πραγματικές ρίζες, οπότε για τη διακρίνουσα της θα ισχύει: 
 . Όμως
. Όμως 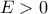 . Οπότε,
. Οπότε, 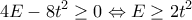 . Άρα, το ελάχιστο εμβαδόν του
. Άρα, το ελάχιστο εμβαδόν του  , ισούται με
, ισούται με 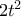 .
.Νομίζω ότι οι πράξεις είναι πάρα πολλές για μια τόσο απλή άσκηση. Ας δούμε κάτι ευκολότερο:nikos_el έγραψε:Η ευθεία, εφ' όσον τέμνει και τους δύο άξονες, ...
 εύκολα βλέπουμε ότι έχει εξίσωση
εύκολα βλέπουμε ότι έχει εξίσωση  . Αφού το
. Αφού το 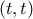 βρίσκεται πάνω στην ευθεία έχουμε
βρίσκεται πάνω στην ευθεία έχουμε  . Λύνοντας ως προς
. Λύνοντας ως προς  έπεται
έπεται  . Τελειώσαμε.
. Τελειώσαμε. και των ορθογωνίων τριγώνων
και των ορθογωνίων τριγώνων  , αν
, αν  η προβολή του
η προβολή του  στην
στην  και
και  η προβολή του
η προβολή του  στην
στην  παίρνουμε
παίρνουμε
 ή
ή 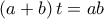 ή
ή 
 , από τις συντεταγμένες επί την αρχήν,
, από τις συντεταγμένες επί την αρχήν,  , που επαληθεύεται για
, που επαληθεύεται για  , άμεσα παίρνουμε το ζητούμενο.
, άμεσα παίρνουμε το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες