 εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .
εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .Νεότατο τμήμα
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
Νεότατο τμήμα
Το τμήμα  εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .
εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .
 εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .
εφάπτεται του ημικυκλίου του σχήματος . Υπολογίστε το μήκος του .Λέξεις Κλειδιά:
- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Νεότατο τμήμα
Από νέο σε νεότατο; Μα κακομαθαίνετε κύριε KARKAR!

Επεξεργασία: Άρση απόκρυψης
.
τελευταία επεξεργασία από george visvikis σε Δευ Μαρ 19, 2018 4:01 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Νεότατο τμήμα
Έστω  .Αν οι
.Αν οι  τέμνονται στο
τέμνονται στο  η τετράδα
η τετράδα  είναι αρμονική .
είναι αρμονική .
Έτσι: . Με Π. Θ. στο
. Με Π. Θ. στο  έχω :
έχω :  .
.
Από Θ. Μενελάου στο και διατέμνουσα
και διατέμνουσα  έχω :
έχω :

 .Αν οι
.Αν οι  τέμνονται στο
τέμνονται στο  η τετράδα
η τετράδα  είναι αρμονική .
είναι αρμονική .Έτσι:
 . Με Π. Θ. στο
. Με Π. Θ. στο  έχω :
έχω :  .
.Από Θ. Μενελάου στο
 και διατέμνουσα
και διατέμνουσα  έχω :
έχω :
Re: Νεότατο τμήμα
Έστω
 η προβολή του
η προβολή του  στην
στην  . Είναι
. Είναι 
Επειδή
 (κάθετες πλευρές) είναι
(κάθετες πλευρές) είναι  και άρα :
και άρα :  . Από την ομοιότητα :
. Από την ομοιότητα : 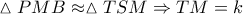
Αφού

- george visvikis
- Επιμελητής
- Δημοσιεύσεις: 13272
- Εγγραφή: Παρ Νοέμ 01, 2013 9:35 am
Re: Νεότατο τμήμα
πρώτα βρίσκω εύκολα ότι
 και στη συνέχεια με Πυθαγόρειο
και στη συνέχεια με Πυθαγόρειο 
απ' όπου παίρνω
 Τα υπόλοιπα με νόμο συνημιτόνων:
Τα υπόλοιπα με νόμο συνημιτόνων:● στο τρίγωνο

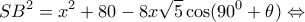


● στο τρίγωνο




● στο τρίγωνο



Παρατήρηση: Από την
 είναι και
είναι και  που σημαίνει ότι η
που σημαίνει ότι η  εφάπτεται στο ημικύκλιο.
εφάπτεται στο ημικύκλιο.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
