Σελίδα 1 από 1
50%
Δημοσιεύτηκε: Παρ Ιαν 12, 2018 8:17 pm
από KARKAR

- 50%.png (16.61 KiB) Προβλήθηκε 576 φορές
Το σημείο

ανήκει στο ημικύκλιο διαμέτρου

. Οι διχοτόμοι των

τέμνονται στο

και τέμνουν το ημικύκλιο στα

αντίστοιχα .
α) Δείξτε ότι :

.
β) Αν το

είναι το μέσο της

, βρείτε την

.
Re: 50%
Δημοσιεύτηκε: Παρ Ιαν 12, 2018 10:20 pm
από Doloros
KARKAR έγραψε: ↑Παρ Ιαν 12, 2018 8:17 pm
50%.pngΤο σημείο

ανήκει στο ημικύκλιο διαμέτρου

. Οι διχοτόμοι των

τέμνονται στο

και τέμνουν το ημικύκλιο στα

αντίστοιχα .
α) Δείξτε ότι :

.
β) Αν το

είναι το μέσο της

, βρείτε την

.
Για το πρώτο ερώτημα.

- 50 στα 100.png (23.58 KiB) Προβλήθηκε 546 φορές
Ας είναι

το σημείο επαφής του εγγεγραμμένου κύκλου του

με τη

.
Θα είναι

. Επειδή Θ. Ν πόλου:

Θα είναι η

μεσοκάθετος στο

άρα αρκεί να δείξουμε ότι :

που ισχύει αφού το

είναι ισοσκελές ορθογώνιο με κάθετες πλευρές

και άρα

.
Στο άλλο θα με απασχολήσει η γεωμετρική κατασκευή του τριγώνου  κι μετά ο υπολογισμός
κι μετά ο υπολογισμός
Είναι

- 50 στα 100_Β ερώτημα.png (28.44 KiB) Προβλήθηκε 537 φορές
Το

είναι τέτοιο ώστε

(Κατασκευή με κύκλο του Απολλώνιου )
Εύκολα μετά

Re: 50%
Δημοσιεύτηκε: Παρ Ιαν 12, 2018 11:41 pm
από Γιώργος Μήτσιος
Χαιρετώ! Για το α' : Το τρίγωνο

είναι
ορθ. και ισοσκελές άρα

.
Για τα
όμοια τρίγωνα

παίρνουμε :
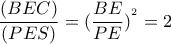

- 13-1-18 ..50 στα 100.PNG (8.09 KiB) Προβλήθηκε 523 φορές
Για το β' : Αν

τότε και

(αφού και τρίγωνο

ορθ. και ισοσκελές)
άρα

. Τότε

..Φιλικά Γιώργος.
Re: 50%
Δημοσιεύτηκε: Σάβ Ιαν 13, 2018 1:53 am
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Παρ Ιαν 12, 2018 8:17 pm
50%.pngΤο σημείο

ανήκει στο ημικύκλιο διαμέτρου

. Οι διχοτόμοι των

τέμνονται στο

και τέμνουν το ημικύκλιο στα

αντίστοιχα .
α) Δείξτε ότι :

.
β) Αν το

είναι το μέσο της

, βρείτε την

.
1.Επειδή

είναι ορθογώνια ισοσκελή, το

είναι μέσον της
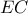
και

τραπέζιο
άρα
 2.
2.Αν επιπλέον
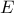
μέσον της

,το

είναι παραλ/μμο

.
Ακόμη,

(βαίνουν σε ίσα τόξα)
Είναι



- 50%.png (20.18 KiB) Προβλήθηκε 517 φορές
Re: 50%
Δημοσιεύτηκε: Σάβ Ιαν 13, 2018 11:18 am
από george visvikis
KARKAR έγραψε: ↑Παρ Ιαν 12, 2018 8:17 pm
50%.pngΤο σημείο

ανήκει στο ημικύκλιο διαμέτρου

. Οι διχοτόμοι των

τέμνονται στο

και τέμνουν το ημικύκλιο στα

αντίστοιχα .
α) Δείξτε ότι :

.
β) Αν το

είναι το μέσο της

, βρείτε την

.

- 50%.png (23.01 KiB) Προβλήθηκε 490 φορές
α)
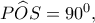
άρα

είναι η πλευρά του τετραγώνου εγγεγραμμένου σε κύκλο ακτίνας

οπότε

κι επειδή τα τρίγωνα

είναι όμοια, θα είναι

β)
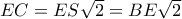
και από νόμο συνημιτόνων στο



οπότε

και
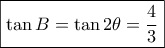
Re: 50%
Δημοσιεύτηκε: Σάβ Ιαν 13, 2018 11:32 am
από Doloros
Παρατήρηση :
Το τρίγωνο  είναι της μορφής
είναι της μορφής  , προκύπτει δε χωρίς τριγωνομετρία( αλλά όχι πιο απλά).
, προκύπτει δε χωρίς τριγωνομετρία( αλλά όχι πιο απλά).
 ανήκει στο ημικύκλιο διαμέτρου
ανήκει στο ημικύκλιο διαμέτρου  . Οι διχοτόμοι των
. Οι διχοτόμοι των 
 και τέμνουν το ημικύκλιο στα
και τέμνουν το ημικύκλιο στα  αντίστοιχα .
αντίστοιχα . .
.  είναι το μέσο της
είναι το μέσο της  , βρείτε την
, βρείτε την  .
. ανήκει στο ημικύκλιο διαμέτρου
ανήκει στο ημικύκλιο διαμέτρου  . Οι διχοτόμοι των
. Οι διχοτόμοι των 
 και τέμνουν το ημικύκλιο στα
και τέμνουν το ημικύκλιο στα  αντίστοιχα .
αντίστοιχα . .
.  είναι το μέσο της
είναι το μέσο της  , βρείτε την
, βρείτε την  .
. το σημείο επαφής του εγγεγραμμένου κύκλου του
το σημείο επαφής του εγγεγραμμένου κύκλου του  με τη
με τη  . Επειδή Θ. Ν πόλου:
. Επειδή Θ. Ν πόλου:
 μεσοκάθετος στο
μεσοκάθετος στο  άρα αρκεί να δείξουμε ότι :
άρα αρκεί να δείξουμε ότι : που ισχύει αφού το
που ισχύει αφού το  είναι ισοσκελές ορθογώνιο με κάθετες πλευρές
είναι ισοσκελές ορθογώνιο με κάθετες πλευρές  και άρα
και άρα  .
. κι μετά ο υπολογισμός
κι μετά ο υπολογισμός είναι τέτοιο ώστε
είναι τέτοιο ώστε  (Κατασκευή με κύκλο του Απολλώνιου )
(Κατασκευή με κύκλο του Απολλώνιου ) 
 είναι ορθ. και ισοσκελές άρα
είναι ορθ. και ισοσκελές άρα .
.  παίρνουμε :
παίρνουμε : 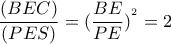
 τότε και
τότε και  (αφού και τρίγωνο
(αφού και τρίγωνο  ορθ. και ισοσκελές)
ορθ. και ισοσκελές) . Τότε
. Τότε  ..Φιλικά Γιώργος.
..Φιλικά Γιώργος. είναι ορθογώνια ισοσκελή, το
είναι ορθογώνια ισοσκελή, το  είναι μέσον της
είναι μέσον της 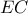 και
και  τραπέζιο
τραπέζιο
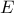 μέσον της
μέσον της  ,το
,το  είναι παραλ/μμο
είναι παραλ/μμο  .
. (βαίνουν σε ίσα τόξα)
(βαίνουν σε ίσα τόξα)

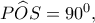 άρα
άρα  οπότε
οπότε 
 είναι όμοια, θα είναι
είναι όμοια, θα είναι 
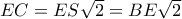 και από νόμο συνημιτόνων στο
και από νόμο συνημιτόνων στο 

 οπότε
οπότε  και
και 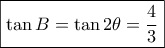
 , προκύπτει δε χωρίς τριγωνομετρία( αλλά όχι πιο απλά).
, προκύπτει δε χωρίς τριγωνομετρία( αλλά όχι πιο απλά).