Α1. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή Λάθος, αν η πρόταση είναι λανθασμένη.
α) Τρία οποιαδήποτε σημεία ορίζουν πάντα μοναδικό επίπεδο.
β) Ένα πολύγωνο λέγεται κανονικό, όταν έχει όλες τις πλευρές του ίσες.
γ) Αν
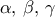 είναι πλευρές τριγώνου
είναι πλευρές τριγώνου  και
και 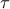 η ημιπερίμετρός του, τότε το εμβαδόν του Ε
η ημιπερίμετρός του, τότε το εμβαδόν του Ε δίνεται από τον τύπο
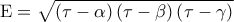 .
.δ) Αν
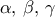 είναι πλευρές τριγώνου
είναι πλευρές τριγώνου  και
και  , τότε
, τότε  .
. ε) Σε κάθε ορθογώνιο τρίγωνο, το τετράγωνο μιας κάθετης πλευράς του είναι ίσο με το γινόμενο
της υποτείνουσας επί την προβολή της πλευράς αυτής στην υποτείνουσα.
Α2. Να αποδείξετε ότι σε κάθε ορθογώνιο τρίγωνο το άθροισμα των τετραγώνων των καθέτων πλευρών του είναι ίσο με το τετράγωνο της υποτείνουσας.
Θέμα Β
Δίνεται τρίγωνο
 με πλευρές
με πλευρές  ,
,  και
και  . Αν
. Αν 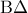 το ύψος του στην πλευρά
το ύψος του στην πλευρά  .
.Β1. Να βρείτε το είδος του τριγώνου ως προς τις γωνίες του.
Β2. Να βρείτε το μήκος της προβολής της πλευράς
 στην
στην 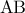 .
.Β3. Να βρείτε το συνημίτονο της γωνίας
 .
.Θέμα Γ
Σε κύκλο κέντρου Ο και ακτίνας R θεωρούμε το εγγεγραμμένο ισοσκελές τραπέζιο

 , με βάσεις
, με βάσεις 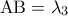 και
και 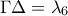 .
Γ1. Να αποδείξετε ότι
.
Γ1. Να αποδείξετε ότι  .
.Γ2. Να αποδείξετε το ύψος
 του τραπεζίου
του τραπεζίου  είναι ίσο με
είναι ίσο με 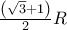 .
.Γ3. Να βρείτε το εμβαδόν του τραπεζίου
 συναρτήσει του
συναρτήσει του  .
.Γ4. Να βρείτε το εμβαδόν του τετραπλεύρου
 συναρτήσει του
συναρτήσει του  . .
. .Θέμα Δ
Στο επίπεδο
 θεωρούμε τετράγωνο
θεωρούμε τετράγωνο  πλευράς
πλευράς  και ευθεία
και ευθεία  κάθετη στο επίπεδο
κάθετη στο επίπεδο  η οποία διέρχεται από το σημείο
η οποία διέρχεται από το σημείο  . Στην ευθεία
. Στην ευθεία  παίρνουμε ευθύγραμμο τμήμα
παίρνουμε ευθύγραμμο τμήμα 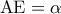 .
.
Δ1. Να αποδείξετε ότι το τρίγωνο
 είναι ισόπλευρο πλευράς
είναι ισόπλευρο πλευράς  .
.Δ2. Να αποδείξετε ότι για την ακτίνα
 του κύκλου που διέρχεται από τις κορυφές του τριγώνου
του κύκλου που διέρχεται από τις κορυφές του τριγώνου  ισχύει
ισχύει  .
.Δ3. Να βρείτε το εμβαδόν του μικτόγραμμου τριγώνου
 συναρτήσει του
συναρτήσει του  .(θεωρούμε το μικτόγραμμο με πλευρά το κυρτό τόξο ΒΔ) .
.(θεωρούμε το μικτόγραμμο με πλευρά το κυρτό τόξο ΒΔ) .
 είναι κάθετη στο επίπεδο θα είναι κάθετη σε κάθε ευθεία του επιπέδου που διέρχεται από το ίχνος της, άρα τα
είναι κάθετη στο επίπεδο θα είναι κάθετη σε κάθε ευθεία του επιπέδου που διέρχεται από το ίχνος της, άρα τα  είναι ίσα, οπότε το τρίγωνο
είναι ίσα, οπότε το τρίγωνο  είναι ισόπλευρο με πλευρά
είναι ισόπλευρο με πλευρά 


 είναι το εμβαδόν του κυκλικού τομέα
είναι το εμβαδόν του κυκλικού τομέα 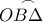 και
και  τα εμβαδά των τριγώνων
τα εμβαδά των τριγώνων  αντίστοιχα,
αντίστοιχα, 

