 είναι ύψος του
είναι ύψος του  και το
και το  τετράγωνο εξωτερικά του . Οι
τετράγωνο εξωτερικά του . Οι  τέμνονται στο
τέμνονται στο 
Να εξεταστεί αν αληθεύει η ισοδυναμία :

Ευχαριστώ , Γιώργος .
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 είναι ύψος του
είναι ύψος του  και το
και το  τετράγωνο εξωτερικά του . Οι
τετράγωνο εξωτερικά του . Οι  τέμνονται στο
τέμνονται στο 

Καλό μεσημέρι! Το απόγευμα η λύση.Γιώργος Μήτσιος έγραψε:Χαίρετε !
21-5-17 Κριτήριο 45άρας !.PNG
Τοείναι ύψος του
και το
τετράγωνο εξωτερικά του . Οι
τέμνονται στο
Να εξεταστεί αν αληθεύει η ισοδυναμία :
Ευχαριστώ , Γιώργος .
 , και έστω
, και έστω  το ορθόκεντρο του
το ορθόκεντρο του  .
. .
. .
.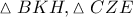 είναι ίσα, άρα
είναι ίσα, άρα  (1).
(1). Από την
Από την  , έχουμε από γνωστή άσκηση
, έχουμε από γνωστή άσκηση  (2).
(2).  .
. Είναι
Είναι 

 (γνωστή πρόταση).
(γνωστή πρόταση). . Προφανώς, το τρίγωνο
. Προφανώς, το τρίγωνο 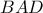 είναι ορθογώνιο και έχει
είναι ορθογώνιο και έχει  , άρα
, άρα  .
. .
. . Τότε
. Τότε  δηλαδή το τετράπλευρο
δηλαδή το τετράπλευρο  είναι
είναι  και άρα το τρίγωνο
και άρα το τρίγωνο  είναι ορθογώνιο και
είναι ορθογώνιο και  να είναι ίσα ως
να είναι ίσα ως  , άρα θα είναι :
, άρα θα είναι :  .
. και αφού
και αφού  θα είναι
θα είναι 
 . Λόγω των
. Λόγω των  το τρίγωνο
το τρίγωνο  είναι ορθογώνιο στο
είναι ορθογώνιο στο  και ισοσκελές άρα
και ισοσκελές άρα  .
.Γιώργος Μήτσιος έγραψε:Χαίρετε !
21-5-17 Κριτήριο 45άρας !.PNG
Τοείναι ύψος του
και το
τετράγωνο εξωτερικά του . Οι
τέμνονται στο
Να εξεταστεί αν αληθεύει η ισοδυναμία :
Ευχαριστώ , Γιώργος .
 προς την
προς την  τέμνει την
τέμνει την  στο
στο  και προφανώς
και προφανώς  και
και  ισοσκελές τραπέζιο
ισοσκελές τραπέζιο εγγράψιμο άρα οι μπλε γωνίες είναι ίσες
εγγράψιμο άρα οι μπλε γωνίες είναι ίσες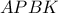 είναι εγγράψιμο συνεπώς είναι ισοσκελές και
είναι εγγράψιμο συνεπώς είναι ισοσκελές και 

 ισοσκελές τραπέζιο κι έτσι όλες οι μπλε γωνίες είναι ίσες
ισοσκελές τραπέζιο κι έτσι όλες οι μπλε γωνίες είναι ίσες εγγράψιμο
εγγράψιμο
 και E σημείο της
και E σημείο της  με
με  . Αν D είναι η προβολή του
. Αν D είναι η προβολή του  στην
στην  , έχουμε
, έχουμε  , οπότε τα τρίγωνα
, οπότε τα τρίγωνα  είναι όμοια καθώς είναι ορθογώνια με λόγο κάθετων πλευρών ίσο με
είναι όμοια καθώς είναι ορθογώνια με λόγο κάθετων πλευρών ίσο με  . Επομένως
. Επομένως , οπότε
, οπότε .
. , κατασκευάζουμε το
, κατασκευάζουμε το  με τον ίδιο τρόπο και μετά κατασκευάζουμε το ορθογώνιο και ισοσκελές τρίγωνο
με τον ίδιο τρόπο και μετά κατασκευάζουμε το ορθογώνιο και ισοσκελές τρίγωνο  με
με  . Με τον ίδιο τρόπο, αποδεικνύουμε ότι τα τρίγωνα
. Με τον ίδιο τρόπο, αποδεικνύουμε ότι τα τρίγωνα  είναι όμοια, οπότε
είναι όμοια, οπότε  , επομένως οι ευθείες
, επομένως οι ευθείες  ταυτίζονται και
ταυτίζονται και  .
.

 .
.

 .
. είναι η
είναι η  ,
,  .
. και
και 
 βρίσκουμε ότι
βρίσκουμε ότι  , δηλαδή η γωνία
, δηλαδή η γωνία  .
. ,
,  , τότε
, τότε 
 .
. , (1) και
, (1) και  , (2).
, (2).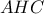 ,
,  υπολογίζουμε ότι
υπολογίζουμε ότι 
 ,
,  συναρτήσει των a, b.
συναρτήσει των a, b. , από όπου προκύπτει ότι γωνία
, από όπου προκύπτει ότι γωνία  .
. είναι ίσοι. Επίσης έχουμε
είναι ίσοι. Επίσης έχουμε  και
και 
 επομένως
επομένως  δηλαδή τα σημεία
δηλαδή τα σημεία  είναι συνευθειακά, επομένως
είναι συνευθειακά, επομένως 
Ανδρέας Πούλος έγραψε:Λύση με τη χρήση των τύπων του εμβαδού τριγώνου.
Ορίζουμε,
, τότε
.
Επίσης,
, (1) και
, (2).
Από ομοιότητα των τριγώνων,
υπολογίζουμε ότι
Με τη χρήση του Πυθαγόρειου θεωρήματος εκφράζουμε τα μήκη,
συναρτήσει των a, b.
Για πρακτικούς λόγους να μην έχουμε τετραγωνικές ρίζες στα μήκη εξισώνουμε τα τετράγωνα του εμβαδού του τριγώνου ABC στους τύπους (1) και (2).
και παίρνουμε ότι, από όπου προκύπτει ότι γωνία
.
 αποτελείται από τις γωνίες
αποτελείται από τις γωνίες  ,
,  .
.
 και
και  .
. .
.Γεια χαρά και πάλι. Ας δούμε και αυτή την άποψη, πάντα για τον εισηγητή Γιώργο:Γιώργος Μήτσιος έγραψε:Χαίρετε !
21-5-17 Κριτήριο 45άρας !.PNG
Τοείναι ύψος του
και το
τετράγωνο εξωτερικά του . Οι
τέμνονται στο
Να εξεταστεί αν αληθεύει η ισοδυναμία :
 (Προφανώς στην ημιευθεία
(Προφανώς στην ημιευθεία  ). Τότε
). Τότε  οπότε
οπότε  συνεπώς
συνεπώς  αφού η κάθετη από το σημείο
αφού η κάθετη από το σημείο  στην
στην 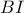 είναι μονοσημάντως ορισμένη.
είναι μονοσημάντως ορισμένη.  και
και 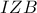 που οδηγεί στο ορθογώνιο και ισοσκελές τρίγωνο
που οδηγεί στο ορθογώνιο και ισοσκελές τρίγωνο  , με
, με  .
. (1)
(1) (2)
(2) (3)
(3) (4)
(4) , δηλαδή η γωνία A = 45.
, δηλαδή η γωνία A = 45. έχουμε ότι
έχουμε ότι  διαγώνιες ίσων ορθογωνίων παραλληλογράμμων
διαγώνιες ίσων ορθογωνίων παραλληλογράμμων , άρα γωνία
, άρα γωνία  .
.Άλλη μια...Γιώργος Μήτσιος έγραψε:Χαίρετε !
21-5-17 Κριτήριο 45άρας !.PNG
Τοείναι ύψος του
και το
τετράγωνο εξωτερικά του . Οι
τέμνονται στο
Να εξεταστεί αν αληθεύει η ισοδυναμία :
Ευχαριστώ , Γιώργος .

 τα
τα  είναι εγράψιμα με
είναι εγράψιμα με  συνευθειακά.
συνευθειακά. εγγράψιμο ,συνεπώς
εγγράψιμο ,συνεπώς 
 εφάπτεται του περίκυκλου του
εφάπτεται του περίκυκλου του 


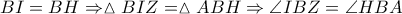 και
και 

 ως ορθογώνιο και ισοσκελές .. λύση που βεβαίως έχει καλυφθεί !
ως ορθογώνιο και ισοσκελές .. λύση που βεβαίως έχει καλυφθεί ! τότε :
τότε :  .
.  οπότε
οπότε  .
. αποδεικνύεται , ως γνωστόν, και αμιγώς Γεωμετρικά .
αποδεικνύεται , ως γνωστόν, και αμιγώς Γεωμετρικά . Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 14 επισκέπτες