 είναι κέντρο του μεγάλου ημικυκλίου ακτίνας
είναι κέντρο του μεγάλου ημικυκλίου ακτίνας 
και η
 εφαπτομένη του μικρού, στο σημείο
εφαπτομένη του μικρού, στο σημείο  . Υπολογίστε το εμβαδόν
. Υπολογίστε το εμβαδόντου τριγώνου
 .
.Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 .
. , άρα η
, άρα η  διχοτομεί την γωνία
διχοτομεί την γωνία  .
.
 .
. και εύκολα
και εύκολα  και
και  .
.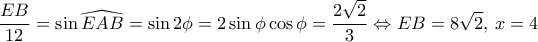 .
. .
. .
. θα δώσει τελικά
θα δώσει τελικά  .
. .
.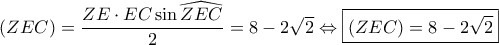 .
.Καλημέρα! ΈστωΦανης Θεοφανιδης έγραψε:
Στο παραπάνω σχήμα τοείναι κέντρο του μεγάλου ημικυκλίου ακτίνας
και ηεφαπτομένη του μικρού, στο σημείο
. Υπολογίστε το εμβαδόν
του τριγώνου.
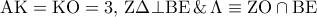
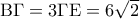 και απ’ το εγγράψιμο
και απ’ το εγγράψιμο 
 και από τα όμοια
και από τα όμοια 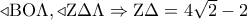

 το κέντρο του μικρού ημικυκλίου και
το κέντρο του μικρού ημικυκλίου και  οι προβολές των
οι προβολές των  στην
στην  . Επειδή τα
. Επειδή τα  αρμονικά συζυγή των
αρμονικά συζυγή των  θα έχω
θα έχω  . Ακόμα
. Ακόμα  και έτσι
και έτσι  θα είναι
θα είναι  .
.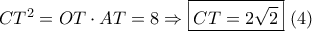

 και προκύπτει :
και προκύπτει : 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης