 και
και  είναι τα μήκη των ισοκλινών προβολών των τμημάτων
είναι τα μήκη των ισοκλινών προβολών των τμημάτων  σε δύο συνεπίπεδες με αυτά
σε δύο συνεπίπεδες με αυτά διακεκριμένες ευθείες
 αντίστοιχα. Να δειχθεί η ισοδυναμία:
αντίστοιχα. Να δειχθεί η ισοδυναμία:  .
.Σημείωση: Στην περίπτωση που δύο σημεία καθένα από τα σύνολα
 και
και  ταυτιστούν (έστω
ταυτιστούν (έστω  )
) τότε ναν δειχθεί ότι:

Στάθης

 , το σημείο ώστε να είναι
, το σημείο ώστε να είναι  και ας είναι
και ας είναι  , οι παράλληλες ( με ίδια διεύθυνση, προς αυτές του σχήματος ) προβολές του τμήματος
, οι παράλληλες ( με ίδια διεύθυνση, προς αυτές του σχήματος ) προβολές του τμήματος  , επί των ευθειών
, επί των ευθειών  , υπό γωνία
, υπό γωνία  , αντιστοίχως.
, αντιστοίχως. και
και 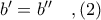 ( προφανές ).
( προφανές ). και
και 

 , σύμφωνα με το γενικευμένο
, σύμφωνα με το γενικευμένο  είναι συνευθειακά.
είναι συνευθειακά. και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. Έστω
Έστω  (σχήμα 1) και
(σχήμα 1) και  , με
, με  σχηματίζουν γωνία
σχηματίζουν γωνία  με την
με την  και
και  σχηματίζουν γωνία
σχηματίζουν γωνία 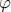 με την
με την  .
. . Με
. Με 
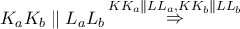 έχουν παράλληλες πλευρές οπότε είναι ομοιόθετα και με
έχουν παράλληλες πλευρές οπότε είναι ομοιόθετα και με  το
το  είναι το εσωτερικό κέντρο ομοιοθεσίας του , άρα
είναι το εσωτερικό κέντρο ομοιοθεσίας του , άρα  διέρχεται από το
διέρχεται από το  συνευθειακά και από την
συνευθειακά και από την  .
. και με δύο πλευρές παράλληλες
και με δύο πλευρές παράλληλες  προκύπτει
προκύπτει  .
. θεωρούμε
θεωρούμε  και ας είναι
και ας είναι  και
και  τα σημεία τομής των εκ των
τα σημεία τομής των εκ των  ευθειών που σχηματίζουν με τις
ευθειών που σχηματίζουν με τις  γωνίες
γωνίες  αντίστοιχα με την ευθεία
αντίστοιχα με την ευθεία 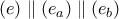 με
με  .
.  . Με
. Με 
 . Με
. Με 
 συνευθειακά , οπότε
συνευθειακά , οπότε  .(προφανώς ισοδυναμία) και το ζητούμενο έχει αποδειχθεί
.(προφανώς ισοδυναμία) και το ζητούμενο έχει αποδειχθεί