Καλημέρα .
Γιώργο και Γιάννη, ευχαριστώ για τις ευέλικτες λύσεις σας .
Για ευκολία πράξεων θέτουμε:

. Θα είναι

.
1.
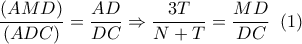
αλλά από το Θ Μενελάου στο τρίγωνο
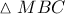
με διατέμνουσα

έχουμε :

Από τις

και αφού

προκύπτει :

.

- Κέρασμα 2_1.png (20.79 KiB) Προβλήθηκε 486 φορές
2. Από την ομοιότητα των

έχουμε :

κι αφού

προκύπτει :

δηλαδή ( αφού

)

Θέτουμε

και λόγω της

έχουμε
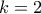
ή

( απορρίπτεται ) δηλαδή

. κατασκευάζουμε τον Απολλώνιο
κύκλο και προσδιορίζουμε το

άρα και το

. Εύκολα βρίσκουμε

.
Δείτε ακόμα ότι τα τρίγωνα

είναι ισοσκελή ορθογώνια.
Φιλικά
Νίκος
 και διαμέτρου
και διαμέτρου  .
.  κινείται πάνω στην ακτίνα
κινείται πάνω στην ακτίνα  ανάμεσα στα
ανάμεσα στα  . Η κάθετη στο
. Η κάθετη στο 
 τέμνει το ημικύκλιο στο
τέμνει το ημικύκλιο στο  . Στο
. Στο  η διάμεσος
η διάμεσος 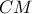 τέμνει το ύψος
τέμνει το ύψος  στο
στο  .
.  επί την
επί την  που τέμνει την
που τέμνει την  στο
στο  .
. είναι
είναι  ;
;
 είναι προφανώς εγγράψιμο άρα
είναι προφανώς εγγράψιμο άρα  και
και  . Έτσι
. Έτσι  \displaystyle{=\dfrac{AM\cdot MD}{ED\cdot EC}}
\displaystyle{=\dfrac{AM\cdot MD}{ED\cdot EC}}
 και
και 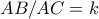 οπότε
οπότε 
 είναι όμοια
είναι όμοια  συνεπώς
συνεπώς  ..
..
 έχουν κοινή την
έχουν κοινή την  δηλ. είναι όμοια με
δηλ. είναι όμοια με  οπότε λόγω και της
οπότε λόγω και της 

 με διατέμνουσα την
με διατέμνουσα την  μας δίνει
μας δίνει 

 , θέτοντας
, θέτοντας  άρα και
άρα και  .Το Π.Θ στο
.Το Π.Θ στο  δίνει
δίνει  .
. παίρνουμε
παίρνουμε  και τότε η
και τότε η  γίνεται τελικά
γίνεται τελικά 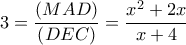
 και συνεπώς
και συνεπώς  ..με άλλα λόγια ..
..με άλλα λόγια ..  .
. και θα υπολογίσω το
και θα υπολογίσω το  συναρτήση της ακτίνας του ημικυκλίου.
συναρτήση της ακτίνας του ημικυκλίου.
 είναι εγράψιμο σε κύκλο άρα
είναι εγράψιμο σε κύκλο άρα 
 . Θα είναι
. Θα είναι  .
.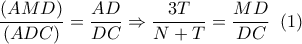 αλλά από το Θ Μενελάου στο τρίγωνο
αλλά από το Θ Μενελάου στο τρίγωνο 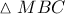 με διατέμνουσα
με διατέμνουσα  έχουμε :
έχουμε :  Από τις
Από τις 
 προκύπτει :
προκύπτει :  .
. έχουμε :
έχουμε :  κι αφού
κι αφού  δηλαδή ( αφού
δηλαδή ( αφού  )
)  Θέτουμε
Θέτουμε  και λόγω της
και λόγω της  έχουμε
έχουμε 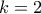 ή
ή  ( απορρίπτεται ) δηλαδή
( απορρίπτεται ) δηλαδή  . κατασκευάζουμε τον Απολλώνιο
. κατασκευάζουμε τον Απολλώνιο  .
.