KARKAR έγραψε:Άσκηση 013Το συνημμένο TETR NANN.png δεν είναι πλέον διαθέσιμο
Σημείο
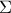
κινείται επί της πλευράς

του τετραγώνου
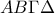
ενώ

είναι το μέσο της

.
Γράφω τα ημικύκλια του σχήματος , με διαμέτρους
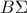
και

, τα οποία τέμνονται στο

1) Δείξτε ότι το

βρίσκεται πάνω στην διαγώνιο

2) Βρείτε τη θέση του
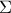
, ώστε το ημικύκλιο διαμέτρου

να διέλθει από το

3) Βρείτε τη θέση του
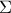
, ώστε το ημικύκλιο διαμέτρου
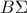
κα εφάπτεται της

Το συνημμένο TETR NANN.png.ggb δεν είναι πλέον διαθέσιμο

- Τετράγωνο_013_1.png (15.22 KiB) Προβλήθηκε 2316 φορές
1. Επειδή οι γωνίες
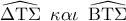
βαίνουν σε ημικύκλια , είναι ορθές άρα
παραπληρωματικές οπότε θα έχουν τις μη κοινές πλευρές τους

αντικείμενες ημιευθείες. Δηλαδή το σημείο

ανήκει στην διαγώνιο

.
2.

- Τετράγωνο_013_2.png (17.38 KiB) Προβλήθηκε 2316 φορές
Τώρα

αφού είναι συμπλήρωμα της γωνίας

. Άμεση συνέπεια: τα
ορθογώνια τρίγωνα

είναι όμοια . Αν η πλευρά του τετραγώνου
είναι
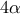
θα έχουμε
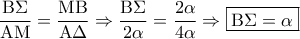
.
3.

- Τετράγωνο_013_3.png (14.95 KiB) Προβλήθηκε 2316 φορές
Αν

το σημείο επαφής του ημικυκλίου διαμέτρου

με την
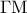
και

το
κέντρο του , τα ορθογώνια τρίγωνα
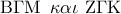
θα είναι προφανώς όμοια .
Ας πούμε

την ακτίνα του πιο πάνω ημικυκλίου . Έχουμε:

. Από το Πυθαγόρειο θεώρημα στο
τρίγωνο

ισχύει :

,
συνεπώς

. Η

τώρα δίδει :

. Με

.
Φιλικά Νίκος
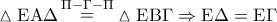 και
και  .
. με:
με: 
 , οπότε
, οπότε  και το
και το  ισόπλευρο.
ισόπλευρο.
 και έστω
και έστω 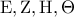 τα μέσα των πλευρών
τα μέσα των πλευρών  αντίστοιχα. Δείξτε ότι το τετράπλευρο
αντίστοιχα. Δείξτε ότι το τετράπλευρο  , που σχηματίζεται απ’ τις τομές των πλευρών
, που σχηματίζεται απ’ τις τομές των πλευρών  , είναι τετράγωνο και ότι
, είναι τετράγωνο και ότι 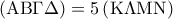 .
. , τέτοιο ώστε
, τέτοιο ώστε  . Αν
. Αν 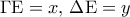 , να δείξετε ότι:
, να δείξετε ότι: .
. .
. είναι, λόγω ισομορφισμού, ο μιγαδικός
είναι, λόγω ισομορφισμού, ο μιγαδικός 
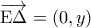 είναι ο μιγαδικός
είναι ο μιγαδικός  . Τότε
. Τότε 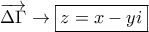 . Αφού δε ο πολλαπλασιασμός με την φανταστική μονάδα
. Αφού δε ο πολλαπλασιασμός με την φανταστική μονάδα  κατά
κατά  θα έχουμε
θα έχουμε  . Μετά απ’
. Μετά απ’ 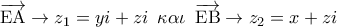 .
.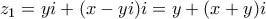 και
και  έχουμε:
έχουμε:  και
και  που είναι και το
που είναι και το  αντίστοιχα, έτσι ώστε
αντίστοιχα, έτσι ώστε  .
. , που σχηματίζεται από τις τομές των πλευρών
, που σχηματίζεται από τις τομές των πλευρών  , είναι τετράγωνο και ότι
, είναι τετράγωνο και ότι  .
. . Να δείξετε ότι
. Να δείξετε ότι  .
.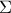 κινείται επί της πλευράς
κινείται επί της πλευράς  του τετραγώνου
του τετραγώνου 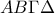 ενώ
ενώ  είναι το μέσο της
είναι το μέσο της  .
.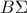 και
και  , τα οποία τέμνονται στο
, τα οποία τέμνονται στο 


 είναι προφανώς ίσα και ορθογώνια (η δικαιολόγηση είναι εύκολη).
είναι προφανώς ίσα και ορθογώνια (η δικαιολόγηση είναι εύκολη). .
. είναι τετράγωνο.
είναι τετράγωνο.
 , έχουμε
, έχουμε
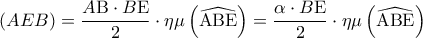 (1)
(1)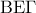 είναι
είναι  (2)
(2)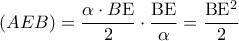 .
. και με πλευρά την
και με πλευρά την  , σχεδιάζω το ισόπλευρο τρίγωνο
, σχεδιάζω το ισόπλευρο τρίγωνο 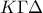 .
.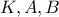 και τη χορδή
και τη χορδή  η οποία διέρχεται
η οποία διέρχεται . Υπολογίστε το μήκος της
. Υπολογίστε το μήκος της 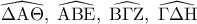 έχουν μέτρο
έχουν μέτρο  ως συμπληρώματα γωνιών
ως συμπληρώματα γωνιών 
 είναι ίσα, αφού έχουν μία κάθετη πλευρά (πλευρές τετραγώνου) και μία αντίστοιχη οξεία γωνία ίσες.
είναι ίσα, αφού έχουν μία κάθετη πλευρά (πλευρές τετραγώνου) και μία αντίστοιχη οξεία γωνία ίσες. είναι
είναι  (υπολογίζοντας το άθροισμα των γωνιών των τριγώνων
(υπολογίζοντας το άθροισμα των γωνιών των τριγώνων  αντίστοιχα.
αντίστοιχα.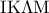 είναι ορθογώνιο παραλληλόγραμμο.
είναι ορθογώνιο παραλληλόγραμμο. , τα τρίγωνα
, τα τρίγωνα  είναι ίσα, οπότε και
είναι ίσα, οπότε και  και
και 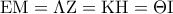 .
. , οπότε
, οπότε  είναι
είναι 
 , οπότε
, οπότε 

 δηλαδή
δηλαδή 

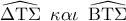 βαίνουν σε ημικύκλια , είναι ορθές άρα
βαίνουν σε ημικύκλια , είναι ορθές άρα 
 ανήκει στην διαγώνιο
ανήκει στην διαγώνιο  .
. αφού είναι συμπλήρωμα της γωνίας
αφού είναι συμπλήρωμα της γωνίας  . Άμεση συνέπεια: τα
. Άμεση συνέπεια: τα  είναι όμοια . Αν η πλευρά του τετραγώνου
είναι όμοια . Αν η πλευρά του τετραγώνου 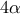 θα έχουμε
θα έχουμε 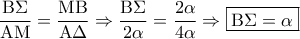 .
.  το σημείο επαφής του ημικυκλίου διαμέτρου
το σημείο επαφής του ημικυκλίου διαμέτρου  με την
με την 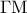 και
και  το
το 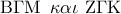 θα είναι προφανώς όμοια .
θα είναι προφανώς όμοια .  την ακτίνα του πιο πάνω ημικυκλίου . Έχουμε:
την ακτίνα του πιο πάνω ημικυκλίου . Έχουμε: . Από το Πυθαγόρειο θεώρημα στο
. Από το Πυθαγόρειο θεώρημα στο  ισχύει :
ισχύει :  ,
,  . Η
. Η  τώρα δίδει :
τώρα δίδει : . Με
. Με  .
. . Να αποδειχθεί ότι για τον κύκλο
. Να αποδειχθεί ότι για τον κύκλο  , ο οποίος διέρχεται απ’ τα
, ο οποίος διέρχεται απ’ τα  και εφάπτεται της πλευράς
και εφάπτεται της πλευράς  στο
στο  .
. .Επειδή
.Επειδή  μέσον της
μέσον της  θα είναι προφανώς
θα είναι προφανώς 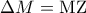 οπότε από το ορθογώνιο τρίγωνο
οπότε από το ορθογώνιο τρίγωνο  θα είναι
θα είναι  είναι μέσον της
είναι μέσον της  (Αφού η
(Αφού η  ως ύψος θα είναι και διάμεσος του ισοσκελούς τριγώνου
ως ύψος θα είναι και διάμεσος του ισοσκελούς τριγώνου  ).Τότε όμως στο ορθογώνιο τρίγωνο
).Τότε όμως στο ορθογώνιο τρίγωνο  η
η  είναι διάμεσος προς την υποτείνουσα ,άρα
είναι διάμεσος προς την υποτείνουσα ,άρα 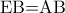
 κόψει την
κόψει την  στο
στο  και τον κύκλο, ακόμα, στο
και τον κύκλο, ακόμα, στο 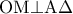 . Θέτω
. Θέτω  . Επειδή τα
. Επειδή τα  είναι όμοια θα έχουμε :
είναι όμοια θα έχουμε :  . Από την δύναμη του σημείου
. Από την δύναμη του σημείου  έχουμε:
έχουμε:  . Συνεπώς
. Συνεπώς 
 η διχοτόμος της
η διχοτόμος της  . Αν
. Αν  , να δείξετε ότι
, να δείξετε ότι  .
. το κέντρο του τετραγώνου
το κέντρο του τετραγώνου

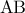 και σημείο
και σημείο  , επί της διαγωνίου
, επί της διαγωνίου  , τέτοιο ώστε
, τέτοιο ώστε  . Να δείξετε ότι το
. Να δείξετε ότι το  είναι ορθογώνιο και ισοσκελές.
είναι ορθογώνιο και ισοσκελές. είναι ίσα επειδή:
είναι ίσα επειδή: ,
, κοινή,
κοινή, .
. .(1)
.(1) ισούται με
ισούται με  με
με  την πλευρά του τετραγώνου.
την πλευρά του τετραγώνου. μας δίνει
μας δίνει  .
.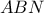 δίνει
δίνει  .Και από τη σχέση (1) παίρνουμε ότι το τρίγωνο
.Και από τη σχέση (1) παίρνουμε ότι το τρίγωνο 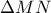 είναι ισοσκελές.
είναι ισοσκελές. παίρνουμε ότι
παίρνουμε ότι  .
. .
.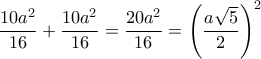 ,άρα στο τρίγωνό μας ισχύει το αντίστροφο του Π.Θ. άρα είναι ορθογώνιο κι έτσι όλα τα ζητούμενα αποδείχθηκαν.
,άρα στο τρίγωνό μας ισχύει το αντίστροφο του Π.Θ. άρα είναι ορθογώνιο κι έτσι όλα τα ζητούμενα αποδείχθηκαν.