 και :
και :  .
.II) Υπάρχει περίπτωση οι ανισώσεις :

και :
 , να έχουν τις ίδιες λύσεις ;
, να έχουν τις ίδιες λύσεις ;Δικαιολογήστε την απάντησή σας . ( Θεωρήστε ότι :
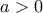 )
)Συντονιστής: exdx
 και :
και :  .
.
 , να έχουν τις ίδιες λύσεις ;
, να έχουν τις ίδιες λύσεις ;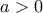 )
) (1) έχει νόημα όταν
(1) έχει νόημα όταν  .
. είναι αδύνατη.
είναι αδύνατη. 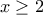 τετραγωνίζουμε ισοδύναμα
τετραγωνίζουμε ισοδύναμα  , οπότε
, οπότε  .
. (2) έχει νόημα όταν
(2) έχει νόημα όταν 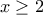 .
.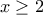 τετραγωνίζουμε ισοδύναμα
τετραγωνίζουμε ισοδύναμα 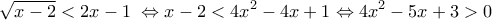 , που ισχύει για κάθε
, που ισχύει για κάθε 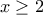 .
.
 (3) έχει νόημα όταν
(3) έχει νόημα όταν  .
.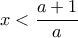 η ανίσωση είναι αδύνατη.
η ανίσωση είναι αδύνατη.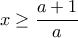 τετραγωνίζουμε ισοδύναμα
τετραγωνίζουμε ισοδύναμα
 .
. 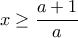 , δεν μπορεί να είναι
, δεν μπορεί να είναι  άρα θα είναι
άρα θα είναι  .
. το διάστημα των λύσεων της (3) είναι το
το διάστημα των λύσεων της (3) είναι το 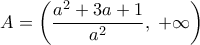
 (4) έχει νόημα όταν
(4) έχει νόημα όταν 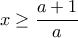 .
.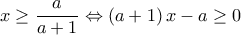 , οπότε τετραγωνίζουμε ισοδύναμα
, οπότε τετραγωνίζουμε ισοδύναμα .
. .
. είναι αρνητική, άρα η ανίσωση ισχύει για κάθε
είναι αρνητική, άρα η ανίσωση ισχύει για κάθε 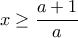 .
. .
. , άρα
, άρα  για κάθε
για κάθε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες