 με
με  να λύσετε την εξίσωση:
να λύσετε την εξίσωση: 
Συντονιστής: exdx
george visvikis έγραψε:Αν θεωρήσουμε γνωστή τη γωνίαμε
να λύσετε την εξίσωση:
![\displaystyle{\sin 5x = \sin x \left [ 2 \cos 2x + 1 + 2 \cos 4x \right ]} \displaystyle{\sin 5x = \sin x \left [ 2 \cos 2x + 1 + 2 \cos 4x \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/b1e2d4bba345f942e3371f7299b657ee.png) και
και ![\displaystyle{\sin 3x = \sin x \left [ 2 \cos 2x + 1 \right ]} \displaystyle{\sin 3x = \sin x \left [ 2 \cos 2x + 1 \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/417037595c3f906aff6bcf687229ef93.png) . Άρα η αρχική εξίσωση γράφεται ως
. Άρα η αρχική εξίσωση γράφεται ως ![\displaystyle{2 \sin x \left [ 2 \cos 2x + 2 \cos 4x + 1 \right ] = \sin x \left [ 2 \cos 2x + 1 \right ] \quad \quad (1)} \displaystyle{2 \sin x \left [ 2 \cos 2x + 2 \cos 4x + 1 \right ] = \sin x \left [ 2 \cos 2x + 1 \right ] \quad \quad (1)}](/forum/ext/geomar/texintegr/latexrender/pictures/6f505d0466e2b2a9810638257fe08345.png) Συνεπώς , γρήγρα γρήγορα έχουμε ότι μία ρίζα της εξίσωσης είναι το
Συνεπώς , γρήγρα γρήγορα έχουμε ότι μία ρίζα της εξίσωσης είναι το  . Για
. Για  μπορούμε να απλοποίησουμε τα ημίτονα αφού δε μηδενίζονται. Συνεπώς η
μπορούμε να απλοποίησουμε τα ημίτονα αφού δε μηδενίζονται. Συνεπώς η  γίνεται:
γίνεται:![\displaystyle{\begin{aligned}
2\left [ 2 \cos 2x + 2 \cos 4x +1 \right ] = 2 \cos 2x +1 &\Leftrightarrow 2 \cos 2x + 1 + 4 \cos 4x =0 \\
&\Leftrightarrow 2\cos 2x + 4 \cos 4x = -1
\end{aligned}} \displaystyle{\begin{aligned}
2\left [ 2 \cos 2x + 2 \cos 4x +1 \right ] = 2 \cos 2x +1 &\Leftrightarrow 2 \cos 2x + 1 + 4 \cos 4x =0 \\
&\Leftrightarrow 2\cos 2x + 4 \cos 4x = -1
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/715b427f52439ce0a30e1f1ab3de34f0.png) Φτάνω μέχρι εδώ , αλλά κόλλησα ... !!
Φτάνω μέχρι εδώ , αλλά κόλλησα ... !! 
Είναιgeorge visvikis έγραψε:Αν θεωρήσουμε γνωστή τη γωνίαμε
να λύσετε την εξίσωση:
 (1).
(1). , για
, για  παίρνουμε
παίρνουμε  (2).
(2). (3).
(3). και με αντικατάσταση στην (3) προκύπτει
και με αντικατάσταση στην (3) προκύπτει  (4).
(4). .
. , οπότε
, οπότε  και
και  . Επίσης
. Επίσης  .
. , άτοπο.
, άτοπο. και όμοια
και όμοια  .
. και έχουμε την
και έχουμε την  (5).
(5). συναρτήσει του
συναρτήσει του  .
. .
. (6).
(6). , έχουμε ως λύση την
, έχουμε ως λύση την  .
. ,
,  ή
ή  .
. .
. .
. . Τότε,
. Τότε,  .
. έχουμε τις ίδιες λύσεις.
έχουμε τις ίδιες λύσεις. .
.Υπόδειξη: Από τον τύπο διπλάσιας γωνίας είναιTolaso J Kos έγραψε:
...
Φτάνω μέχρι εδώ , αλλά κόλλησα ... !!


 .
. συναρτήσει του
συναρτήσει του  .
.



 .
. .
.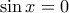 , έχουμε ως λύση την
, έχουμε ως λύση την  .
. έχουμε
έχουμε  και αν
και αν  ,
,  ή
ή  .
. ή
ή  .
. έχουμε
έχουμε  ή
ή  .
. έχουμε
έχουμε 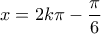 ή
ή  .
. .
.
 .
. στην πρώτη ανάρτηση του Ορέστη. Θα χρησιμοποιήσω τους τύπους:
στην πρώτη ανάρτηση του Ορέστη. Θα χρησιμοποιήσω τους τύπους:  και
και 

![\displaystyle{\sin x[2(1 + \cos 2x)\cos 2x + 6{\cos ^2}x - 3] = 0 \Leftrightarrow \sin x\left( {8{{\cos }^2}2x + 2\cos 2x - 3} \right) = 0 \Leftrightarrow } \displaystyle{\sin x[2(1 + \cos 2x)\cos 2x + 6{\cos ^2}x - 3] = 0 \Leftrightarrow \sin x\left( {8{{\cos }^2}2x + 2\cos 2x - 3} \right) = 0 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/e63f38ca054c99d7dbc780679bc15a1f.png)
 απ' όπου παίρνω τις τελικές λύσεις:
απ' όπου παίρνω τις τελικές λύσεις: ή
ή  ή
ή 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες