 περιττός.
περιττός.1) Να δείξετε ότι

2) Να δείξετε ότι για
 η εξίσωση
η εξίσωση 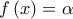 έχει λύση
έχει λύσηεάν-ν
![\alpha \in \left( { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right) \alpha \in \left( { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right)](/forum/ext/geomar/texintegr/latexrender/pictures/fb57bb9872e3268a9c02b8dca40575ef.png) .
.3) Ποιο το σύνολο τιμών της
 ;
;4) Να λύσετε την εξίσωση :

Συντονιστής: exdx
Καλησπέρα. Μια προσπάθεια...erxmer έγραψε:Δίνεται η συνάρτηση με τύποπεριττός.
1) Να δείξετε ότι
2) Να δείξετε ότι γιαη εξίσωση
έχει λύση
εάν-ν.
3) Ποιο το σύνολο τιμών της;
4) Να λύσετε την εξίσωση :
 ισχύει
ισχύει 




 . Ισχύει.
. Ισχύει. ισχύει
ισχύει 




 . Ισχύει.
. Ισχύει. αποδείξαμε ότι
αποδείξαμε ότι  . Είναι
. Είναι  .
.  , για το διάστημα
, για το διάστημα  , παρουσιάζει στην θέση
, παρουσιάζει στην θέση  ολικό ελάχιστο, το
ολικό ελάχιστο, το .
.  .
. αποδείξαμε ότι
αποδείξαμε ότι  . Είναι
. Είναι  .
.  , για το διάστημα
, για το διάστημα  , παρουσιάζει στην θέση
, παρουσιάζει στην θέση  ολικό μέγιστο, το
ολικό μέγιστο, το  .
. ![\forall a\in\left (-\infty , -2\right ], \exists x_{1}\in\left (-\infty ,0\right ) :f(x_{1})=a \forall a\in\left (-\infty , -2\right ], \exists x_{1}\in\left (-\infty ,0\right ) :f(x_{1})=a](/forum/ext/geomar/texintegr/latexrender/pictures/68852910ef317ac0cb86792ab0635e6b.png) .
. είναι το
είναι το ![\left( { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right) \left( { - \infty , - 2} \right] \cup \left[ {2, + \infty } \right)](/forum/ext/geomar/texintegr/latexrender/pictures/5bbb742468cee0fd4a14711dd349ee38.png) .
. η εξίσωση είναι αδύνατη.
η εξίσωση είναι αδύνατη. , διαιρώντας δια
, διαιρώντας δια  , έχουμε :
, έχουμε :




 . Έστω ότι
. Έστω ότι 



 . Άτοπο.
. Άτοπο. και
και  έχουμε
έχουμε  .
.  και
και  έχουμε
έχουμε  .
.  .
. , να παραγωγίσουμε και να αποδείξουμε εύκολα
, να παραγωγίσουμε και να αποδείξουμε εύκολα  , ολικό ελάχιστο το
, ολικό ελάχιστο το 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες