 και
και  .
.Να δείξετε ότι οι κοινοί όροι των δύο αυτών προόδων σχηματίζουν μια νέα αριθμητική πρόοδο.
Συντονιστής: stranton
 και
και  .
.Οι ακολουθίες αυτές γράφονται με συντομία:hlkampel έγραψε:Δίνονται οι αριθμητικές πρόοδοικαι
.
Να δείξετε ότι οι κοινοί όροι των δύο αυτών προόδων σχηματίζουν μια νέα αριθμητική πρόοδο.


 τέτοια ώστε:
τέτοια ώστε:



 της πρώτης ακολουθίας
της πρώτης ακολουθίας  της δεύτερης ακολουθίας.
της δεύτερης ακολουθίας.  που προκύπτει για την τιμή
που προκύπτει για την τιμή  και
και  .
. hlkampel έγραψε:Δίνονται οι αριθμητικές πρόοδοικαι
.
Να δείξετε ότι οι κοινοί όροι των δύο αυτών προόδων σχηματίζουν μια νέα αριθμητική πρόοδο.
 αν έχουν κοινούς
αν έχουν κοινούς  με
με  που έχει μια
που έχει μια  . Όλες οι λύσεις δίδονται από τις
. Όλες οι λύσεις δίδονται από τις  και άρα οι κοινοί όροι είναι
και άρα οι κοινοί όροι είναι 
 και διαφορά
και διαφορά  .
.Διονύσιε, ναι, έχεις δίκιο.Διονύσιος Αδαμόπουλος έγραψε:Νομίζω πως πάντα όταν δυο αριθμητικές πρόοδοι έχουν κοινούς όρους, τότε αυτοί θα ανήκουν σε αριθμητική πρόοδο

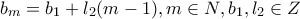

 πρώτοι μεταξύ των, τότε
πρώτοι μεταξύ των, τότε 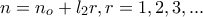 και
και 
 μια μερική λύση της (1).
μια μερική λύση της (1). 


Σωστός!Διονύσιος Αδαμόπουλος έγραψε:Νομίζω πως πάντα όταν δυο αριθμητικές πρόοδοι έχουν κοινούς όρους, τότε αυτοί θα ανήκουν σε αριθμητική πρόοδο
Διονύσιος Αδαμόπουλος έγραψε:Νομίζω πως πάντα όταν δυο αριθμητικές πρόοδοι έχουν κοινούς όρους, τότε αυτοί θα ανήκουν σε αριθμητική πρόοδο
Αρκεί ένας. Αν υπάρχει ένας αριθμός με τις σωστές ισοτιμίες, τότε υπάρχουν άπειροι.hlkampel έγραψε:για το γενικό με την προϋπόθεση (νομίζω) ότι οι κοινοί όροι είναι περισσότεροι από δύο.
Καλησπέρα.dement έγραψε:Αρκεί ένας. Αν υπάρχει ένας αριθμός με τις σωστές ισοτιμίες, τότε υπάρχουν άπειροι.hlkampel έγραψε:για το γενικό με την προϋπόθεση (νομίζω) ότι οι κοινοί όροι είναι περισσότεροι από δύο.
(Θεωρούμε πάντα πως οι αριθμητικές πρόοδοι αποτελούνται από ακεραίους).
 και
και 
Καλησπέρα.hlkampel έγραψε:Καλησπέρα.dement έγραψε:Αρκεί ένας. Αν υπάρχει ένας αριθμός με τις σωστές ισοτιμίες, τότε υπάρχουν άπειροι.hlkampel έγραψε:για το γενικό με την προϋπόθεση (νομίζω) ότι οι κοινοί όροι είναι περισσότεροι από δύο.
(Θεωρούμε πάντα πως οι αριθμητικές πρόοδοι αποτελούνται από ακεραίους).
Αναφέρομαι σε προόδους της μορφής:
και
 και
και 
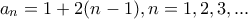 και
και 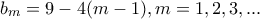


 έχει άπειρες λύσεις που δίνονται από τον τύπο:
έχει άπειρες λύσεις που δίνονται από τον τύπο:
 , προκύπτει ότι οι μόνες λύσεις της (2)
, προκύπτει ότι οι μόνες λύσεις της (2)  και οι οποίες δίνουν τις
και οι οποίες δίνουν τις 
 οι οποίοι αντιστοιχούν στους
οι οποίοι αντιστοιχούν στους 
 είναι η μονάδα
είναι η μονάδα
Ακριβώς. Αν θέλουμε ένα χειροποιαστό παράδειγμα είναι οι πρόοδοιKDORTSI έγραψε:
Αν τώρα στο ερώτημά μας, δηλαδή στην εύρεση των κοινών όρων δύο αριθμητικών προόδων με όρους στο
τότε όλα τα ανωτέρω που στηρίζονται στη διοφαντική ανάλυση δεν έχουν λόγο και το πρόβλημα αποκτά κάθε φορά
την ιδιαιτερότητά του.
 και
και  , οι οποίες έχουν μόνο ένα κοινό στοιχείο (το
, οι οποίες έχουν μόνο ένα κοινό στοιχείο (το  )
)Μιχάλη ευχαριστώ για τα χαιρετίσματα και για την προσοχή που έδειξες στα γραφόμενά μου,Mihalis_Lambrou έγραψε:Κώστα, τα θερμά μου χαιρετίσματα.
Ακριβώς. Αν θέλουμε ένα χειροποιαστό παράδειγμα είναι οι πρόοδοιKDORTSI έγραψε:
Αν τώρα στο ερώτημά μας, δηλαδή στην εύρεση των κοινών όρων δύο αριθμητικών προόδων με όρους στο
τότε όλα τα ανωτέρω που στηρίζονται στη διοφαντική ανάλυση δεν έχουν λόγο και το πρόβλημα αποκτά κάθε φορά
την ιδιαιτερότητά του.και
, οι οποίες έχουν μόνο ένα κοινό στοιχείο (το
)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 29 επισκέπτες