Με αφορμή το πρόβλημα
εδώ ας δούμε και μία γενίκευση προς λίγο πιο διαφορετική κατεύθυνση. Σε ένα φυλλάδιο με τίτλο "Πραγματική Αλγεβρική Γεωμετρία" (βλέπε
εδώ στα ρώσικα) που απευθύνεται πρωτίστως σε μαθητές μεγάλων τάξεων ως εκλαϊκευμένες διαλέξεις ο V.Arnold παραθέτει διάφορες έννοιες της αλγεβρικής γεωμετρίας. Στο τελικό κεφάλαιο σαν ένα πρόβλημα που μπορεί κάποιος να ασχοληθεί και με σχολικά μέσα αποδεικνύει το παρακάτω θεώρημα. Μπορεί να το προσπαθήσει όποιος θέλει.
Θεώρημα: Το επίπεδο δεν μπορεί να διαμεριστεί σε  χωρία με
χωρία με  διαφορετικές ευθείες, αν
διαφορετικές ευθείες, αν  ,καθώς και αν
,καθώς και αν 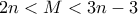 .
.
Στην απόκρυψη είναι διάφορες επιμέρους προτάσεις που οδήγουν στην απόδειξη.
Θεωρούμε τους παρακάτω συμβολισμούς.
Συμβολίζουμε με

τον μέγιστο αριθμό παράλληλων μεταξύ τους ευθειών στην υπό εξέταση τοποθέτηση των

ευθειών.
Συμβολίζουμε με

τον μέγιστο αριθμό ευθειών που διέρχονται από το ίδιο σημείο, σε μια τοποθέτηση.
Πρόταση 1. Αν

, τότε ο αρθμός των χωρίων είναι

.
Πρόταση 2. Αν

, ο αριθμός των χωρίων είναι

.
Πρόταση 3. Αν

, τότε ο αριθμός των χωρίων είναι είτε
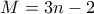
, είτε
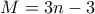
.
Πρόταση 4. Αν

, ο αριθμός των χωρίων είναι

.
Πρόταση 5. Αν

, ο αριθμός των χωρίων είναι
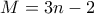
ή
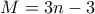
.
Πρόταση 6. Αν
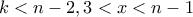
τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα
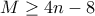
. Και αν μόνο
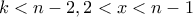
τότε

.
Πρόταση 7. Αν

(δηλαδή ανά τρεις οι ευθείες δεν έχουν κοινό σημείο) και
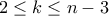
, τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα
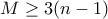
.
Πρόταση 8. Αν

(δηλαδή ανα τρεις δεν διέρχονται από το ίδιο σημείο και δεν υπάρχει ζευγος παράλληλων ευθειών) τότε ο αριθμός των χωρίων είναι ο μέγιστος δυνατός για δεδομένο

,
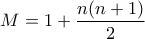
.
Σαν υστερόγραφο παραθέτω τα όσα αναφέρει ο συγγραφέας για την ιστορία του προβλήματος
«αναφέρθηκα εδώ σε αυτό το στοιχειώδες πρόβλημα κυριώς για να βοηθήσω τους μαθητές στην λύση του. Ελπίζω, ο αναγνώστης να δημοσιεύσει αυτή την λύση.
Πρόσφατα ο A.Givental μετέφρασε στα αγγλικά το αξιόλογο εγχειρίδιο ¨
Γεωμετρία¨ του Κισέλεβ. Διαβάζοντας την μετάφραση αυτού του βιβλίου στο Μπέρκλεϊ τον Απρίλιο του 2007, με το οποίο ήμουν πολύ καλά εξοικειωμένος, συνειδητοποίησα ότι δεν ήμουν σε θέση να λύσω ένα από τα προβλήματα (παρότι στα παιδικά μου χρόνια τα είχα λύσει όλα). Στην σύγκριση που έκανα αποδείχθηκε ότι αυτό το πρόβλημα στο πρωτότυπο δεν υπήρχε και προστέθηκε από τον μεταφραστή. Η διατύπωση ήταν η εξής: Πόσες ευθείες πρέπει να διαλέξουμε, ώστε να μπορούμε να διαμερίσουμε το επίπεδο σε 5 χωρία;
Τελικά, ερχόμενος(από την Γαλλία στο Μπέρκλεϊ ) κατευθείαν γενίκευσα το πρόβλημα, εξετάζοντας οποιοδήποτε

αριθμό ευθειών και

χωρίων. Έτσι προέκυψε το παραπάνω θεώρημα, ανοίγοντας πιστεύω ένα ολόκληρο πεδίο δραστηριοτήτων, για τους μαθητές που αγαπούν τα μαθηματικά.»
 χωρία με
χωρία με  διαφορετικές ευθείες, αν
διαφορετικές ευθείες, αν  ,καθώς και αν
,καθώς και αν 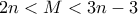 .
.  αριθμό ευθειών και
αριθμό ευθειών και  χωρίων. Έτσι προέκυψε το παραπάνω θεώρημα, ανοίγοντας πιστεύω ένα ολόκληρο πεδίο δραστηριοτήτων, για τους μαθητές που αγαπούν τα μαθηματικά.»
χωρίων. Έτσι προέκυψε το παραπάνω θεώρημα, ανοίγοντας πιστεύω ένα ολόκληρο πεδίο δραστηριοτήτων, για τους μαθητές που αγαπούν τα μαθηματικά.»
 τον μέγιστο αριθμό παράλληλων μεταξύ τους ευθειών στην υπό εξέταση τοποθέτηση των
τον μέγιστο αριθμό παράλληλων μεταξύ τους ευθειών στην υπό εξέταση τοποθέτηση των  τον μέγιστο αριθμό ευθειών που διέρχονται από το ίδιο σημείο, σε μια τοποθέτηση.
τον μέγιστο αριθμό ευθειών που διέρχονται από το ίδιο σημείο, σε μια τοποθέτηση.  , τότε ο αρθμός των χωρίων είναι
, τότε ο αρθμός των χωρίων είναι  .
. , ο αριθμός των χωρίων είναι
, ο αριθμός των χωρίων είναι  .
. , τότε ο αριθμός των χωρίων είναι είτε
, τότε ο αριθμός των χωρίων είναι είτε 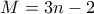 , είτε
, είτε 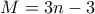 .
. , ο αριθμός των χωρίων είναι
, ο αριθμός των χωρίων είναι  , ο αριθμός των χωρίων είναι
, ο αριθμός των χωρίων είναι 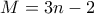 ή
ή 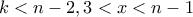 τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα
τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα 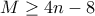 . Και αν μόνο
. Και αν μόνο 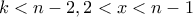 τότε
τότε  .
. (δηλαδή ανά τρεις οι ευθείες δεν έχουν κοινό σημείο) και
(δηλαδή ανά τρεις οι ευθείες δεν έχουν κοινό σημείο) και 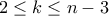 , τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα
, τότε ο αριθμός των χωρίων ικανοποιεί την ανισότητα 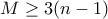 .
. (δηλαδή ανα τρεις δεν διέρχονται από το ίδιο σημείο και δεν υπάρχει ζευγος παράλληλων ευθειών) τότε ο αριθμός των χωρίων είναι ο μέγιστος δυνατός για δεδομένο
(δηλαδή ανα τρεις δεν διέρχονται από το ίδιο σημείο και δεν υπάρχει ζευγος παράλληλων ευθειών) τότε ο αριθμός των χωρίων είναι ο μέγιστος δυνατός για δεδομένο 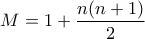 .
.