Γ.-Σ. Σμυρλής έγραψε:ΠΡΟΒΛΗΜΑ. Δίδεται τετράπλευρο μὲ μήκη πλευρῶν  , τὸ ὁποῖο εἶναι περιγράψιμο, δηλαδή, ὑπάρχει κύκλος ἐντὸς αὐτοῦ, ὁ ὁποῖος ἐφάπτεται καὶ μὲ τὶς τέσσερίς του πλευρές. Ἂν τὸ ἐμβαδόν του ἰσοῦται μὲ
, τὸ ὁποῖο εἶναι περιγράψιμο, δηλαδή, ὑπάρχει κύκλος ἐντὸς αὐτοῦ, ὁ ὁποῖος ἐφάπτεται καὶ μὲ τὶς τέσσερίς του πλευρές. Ἂν τὸ ἐμβαδόν του ἰσοῦται μὲ  , δείξατε ὅτι τὸ τετράπλευρο αὐτὸ εἶναι ἐγγράψιμο.
, δείξατε ὅτι τὸ τετράπλευρο αὐτὸ εἶναι ἐγγράψιμο.
Καλημέρα!
Έστω

περιγράψιμο τετράπλευρο με διαδοχικές πλευρές

διαγωνίους
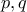
, εμβαδόν

, ημιπερίμετρο

και ακτίνα εγγεγραμμένου κύκλου

. Είναι:



.
Έστω ότι δεν είναι εγγράψιμο. Τότε από την ανισότητα του Πτολεμαίου:

και από την

,

που είναι άτοπο. Άρα το τετράπλευρο είναι εγγράψιμο.
ΥΓ. Όταν άρχισα να πληκτρολογώ δεν υπήρχε η ΣΗΜΕΙΩΣΗ (Θα κοιτάξω για στοιχειωδέστερη λύση).
 , τὸ ὁποῖο εἶναι περιγράψιμο, δηλαδή, ὑπάρχει κύκλος ἐντὸς αὐτοῦ, ὁ ὁποῖος ἐφάπτεται καὶ μὲ τὶς τέσσερίς του πλευρές. Ἂν τὸ ἐμβαδόν του ἰσοῦται μὲ
, τὸ ὁποῖο εἶναι περιγράψιμο, δηλαδή, ὑπάρχει κύκλος ἐντὸς αὐτοῦ, ὁ ὁποῖος ἐφάπτεται καὶ μὲ τὶς τέσσερίς του πλευρές. Ἂν τὸ ἐμβαδόν του ἰσοῦται μὲ  , δείξατε ὅτι τὸ τετράπλευρο αὐτὸ εἶναι ἐγγράψιμο.
, δείξατε ὅτι τὸ τετράπλευρο αὐτὸ εἶναι ἐγγράψιμο.
 περιγράψιμο τετράπλευρο με διαδοχικές πλευρές
περιγράψιμο τετράπλευρο με διαδοχικές πλευρές 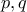 , εμβαδόν
, εμβαδόν  , ημιπερίμετρο
, ημιπερίμετρο  και ακτίνα εγγεγραμμένου κύκλου
και ακτίνα εγγεγραμμένου κύκλου  . Είναι:
. Είναι:

 .
.
 που είναι άτοπο. Άρα το τετράπλευρο είναι εγγράψιμο.
που είναι άτοπο. Άρα το τετράπλευρο είναι εγγράψιμο.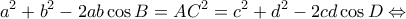

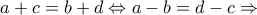









 και το ζητούμενο έπεται.
και το ζητούμενο έπεται.