 :
: .
.Φιλικά,
Νίκος
Συντονιστές: achilleas, emouroukos, silouan
 :
: .
.Έστω
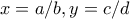 οι ρητοί σε ανάγωγες μορφές. χωρίς βλάβη
οι ρητοί σε ανάγωγες μορφές. χωρίς βλάβη 
 , άρα
, άρα 
 , άρα για κάθε πρώτο
, άρα για κάθε πρώτο  είναι
είναι  από όπου εύκολα συμπεραίνουμε πως
από όπου εύκολα συμπεραίνουμε πως  και έτσι
και έτσι  , επομένως η εξίσωση γίνεται
, επομένως η εξίσωση γίνεται και είναι
και είναι 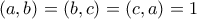 (γνωρίζουμε ήδη τα δύο πρώτα και αν υπήρχε πρώτος
(γνωρίζουμε ήδη τα δύο πρώτα και αν υπήρχε πρώτος 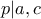 τότε
τότε 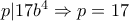 αλλά τότε θα ήταν και
αλλά τότε θα ήταν και  άτοπο)
άτοπο) . Τότε
. Τότε 

 αφού
αφού 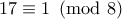 άρα
άρα  τετραγωνικό κατάλοιπο
τετραγωνικό κατάλοιπο 
 έχουμε
έχουμε  η οποία όμως είναι αδύνατη
η οποία όμως είναι αδύνατη Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες