 , με ύψη
, με ύψη  και ακτίνα περιγεγραμμένου κύκλου
και ακτίνα περιγεγραμμένου κύκλου  , να δείξετε ότι :
, να δείξετε ότι :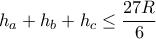 .
.Συντονιστές: achilleas, emouroukos, silouan
 , με ύψη
, με ύψη  και ακτίνα περιγεγραμμένου κύκλου
και ακτίνα περιγεγραμμένου κύκλου  , να δείξετε ότι :
, να δείξετε ότι :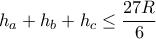 .
.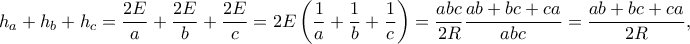

 με τη δεξία να είναι π.χ. συνέπεια της
με τη δεξία να είναι π.χ. συνέπεια της 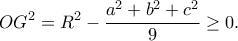


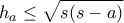

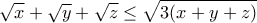

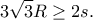

Μεταφέρθηκε στους Seniors.matha έγραψε:
Θεωρώ ότι δεν είναι επιπέδου διαγωνισμών γυμνασίου, τουλάχιστον για τα ελληνικά δεδομένα.

 έπεται το ζητούμενο.
έπεται το ζητούμενο.Για ξανακοίτα την τελευταία ανισότητα.ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Mια διαφορετική προσσέγγιση για το θέμα...
Είναι γνωστό:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες