 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε  .
.Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε  .
.



![\displaystyle{P\left( {0,y} \right) \Rightarrow f\left( y \right)f\left( { - y} \right) = {f^2}\left( y \right) \Rightarrow \left[ {f\left( y \right) = 0 \vee f\left( y \right) = f\left( { - y} \right)} \right]} \displaystyle{P\left( {0,y} \right) \Rightarrow f\left( y \right)f\left( { - y} \right) = {f^2}\left( y \right) \Rightarrow \left[ {f\left( y \right) = 0 \vee f\left( y \right) = f\left( { - y} \right)} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/0bd975622663addbabc03bfb355bb961.png) για κάθε
για κάθε  .
.  για κάθε
για κάθε  , οπότε αν
, οπότε αν  για κάποιο
για κάποιο  , τότε θα είναι και
, τότε θα είναι και 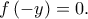 Επομένως, ισχύει
Επομένως, ισχύει  για κάθε
για κάθε  , δηλαδή η συνάρτηση
, δηλαδή η συνάρτηση  είναι άρτια.
είναι άρτια.
![\displaystyle{P\left( {x, - x} \right) \Rightarrow 2\left( {f\left( x \right) - {x^2}} \right)f\left( {4x} \right) = 0 \Rightarrow \left[ {f\left( {4x} \right) = 0 \vee f\left( x \right) = {x^2}} \right]} \displaystyle{P\left( {x, - x} \right) \Rightarrow 2\left( {f\left( x \right) - {x^2}} \right)f\left( {4x} \right) = 0 \Rightarrow \left[ {f\left( {4x} \right) = 0 \vee f\left( x \right) = {x^2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/625246e3321b0207fc9ba70404b97439.png) για κάθε
για κάθε  .
.


 για κάθε
για κάθε  .
. και άρα
και άρα ![\displaystyle{\left[ {f\left( {x} \right) = 0 \vee f\left( x \right) = {x^2}} \right]} \displaystyle{\left[ {f\left( {x} \right) = 0 \vee f\left( x \right) = {x^2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b3cc452a538489e56cbb8754fe81edf0.png) για κάθε
για κάθε  .
. Έστω ότι υπάρχουν
Έστω ότι υπάρχουν  τέτοιοι, ώστε
τέτοιοι, ώστε  και
και  Επειδή η
Επειδή η  είναι άρτια, μπορούμε να υποθέσουμε δίχως βλάβη της γενικότητας ότι
είναι άρτια, μπορούμε να υποθέσουμε δίχως βλάβη της γενικότητας ότι  και
και 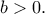
 ,
,![\displaystyle{P\left( {\frac{{3b - a}}{8},\frac{{b - 3a}}{8}} \right) \Rightarrow {b^2}\left[ {f\left( {\frac{{b - 3a}}{8}} \right) + \frac{{\left( {3b - a} \right)\left( {b - 3a} \right)}}{{64}}} \right] = {f^2}\left( {\frac{{b - a}}{2}} \right) \Rightarrow } \displaystyle{P\left( {\frac{{3b - a}}{8},\frac{{b - 3a}}{8}} \right) \Rightarrow {b^2}\left[ {f\left( {\frac{{b - 3a}}{8}} \right) + \frac{{\left( {3b - a} \right)\left( {b - 3a} \right)}}{{64}}} \right] = {f^2}\left( {\frac{{b - a}}{2}} \right) \Rightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/8044705992b5857460d7ba45c3893fe4.png)
![\displaystyle{ \Rightarrow {b^2}\left[ {\underbrace {f\left( {\frac{{b - 3a}}{8}} \right)}_{ \ge 0} + \underbrace {\frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}}_{ > 0}} \right] = {f^2}\left( {\frac{{b - a}}{2}} \right) \Rightarrow {f^2}\left( {\frac{{b - a}}{2}} \right) > 0 \Rightarrow } \displaystyle{ \Rightarrow {b^2}\left[ {\underbrace {f\left( {\frac{{b - 3a}}{8}} \right)}_{ \ge 0} + \underbrace {\frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}}_{ > 0}} \right] = {f^2}\left( {\frac{{b - a}}{2}} \right) \Rightarrow {f^2}\left( {\frac{{b - a}}{2}} \right) > 0 \Rightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/eac622447cc7f76566051a044a4fff18.png)
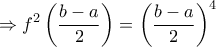 .
.![\displaystyle{{\left( {\frac{{b - a}}{2}} \right)^4} = {b^2}\left[ {f\left( {\frac{{b - 3a}}{8}} \right) + \frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}} \right] \le {b^2}\left[ {{{\left( {\frac{{b - 3a}}{8}} \right)}^2} + \frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}} \right] \Rightarrow } \displaystyle{{\left( {\frac{{b - a}}{2}} \right)^4} = {b^2}\left[ {f\left( {\frac{{b - 3a}}{8}} \right) + \frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}} \right] \le {b^2}\left[ {{{\left( {\frac{{b - 3a}}{8}} \right)}^2} + \frac{{3{a^2} + 3{b^2} - 10ab}}{{64}}} \right] \Rightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/5dfb03ee16f7db7398651da05292f685.png)


 για κάθε
για κάθε  ή
ή  για κάθε
για κάθε  , συναρτήσεις που επαληθεύουν τη δοσμένη συναρτησιακή σχέση.
, συναρτήσεις που επαληθεύουν τη δοσμένη συναρτησιακή σχέση.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες