 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Συντονιστές: achilleas, emouroukos, silouan
 τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
 .
. ) η δοσμένη συναρτησιακή σχέση.
) η δοσμένη συναρτησιακή σχέση.  είναι επί, θα υπάρχει
είναι επί, θα υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  .
. )
)  , βρίσκουμε ότι
, βρίσκουμε ότι  .
. )
)  και
και  , βρίσκουμε ότι
, βρίσκουμε ότι  .
. )
)  , βρίσκουμε ότι για κάθε
, βρίσκουμε ότι για κάθε  ισχύει:
ισχύει: (1).
(1). είναι επί, θα υπάρχει
είναι επί, θα υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  .
.  )
)  και
και  , βρίσκουμε ότι
, βρίσκουμε ότι  (2).
(2). )
)  και
και  , βρίσκουμε ότι
, βρίσκουμε ότι  , οπότε
, οπότε  (3).
(3). .
. ) όπου
) όπου  το
το  και όπου
και όπου  το
το  , βρίσκουμε ότι για κάθε
, βρίσκουμε ότι για κάθε  ισχύει:
ισχύει: (4).
(4). ) γράφεται:
) γράφεται: .
. είναι επί, η τελευταία σχέση δίνει ότι για κάθε
είναι επί, η τελευταία σχέση δίνει ότι για κάθε  ισχύει:
ισχύει: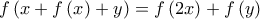 (5).
(5). , βρίσκουμε ότι για κάθε
, βρίσκουμε ότι για κάθε  ισχύει:
ισχύει: (6).
(6). , βρίσκουμε ότι για κάθε
, βρίσκουμε ότι για κάθε  ισχύει:
ισχύει: (7).
(7). το
το  , βρίσκουμε ότι για κάθε
, βρίσκουμε ότι για κάθε  ισχύει:
ισχύει: (8).
(8). ισχύει:
ισχύει: .
. είναι επί, θα έχουμε ότι για κάθε
είναι επί, θα έχουμε ότι για κάθε  ισχύει:
ισχύει: (9).
(9). το
το  και χρησιμοποιώντας την (4) βρίσκουμε ότι:
και χρησιμοποιώντας την (4) βρίσκουμε ότι: ,
, για κάθε
για κάθε  , η οποία επαληθεύει την (
, η οποία επαληθεύει την ( ).
). τέτοιες ώστε
τέτοιες ώστε  για κάθε
για κάθε 
Επαναφορά!socrates έγραψε:Να προσδιορίσετε όλες τις επί συναρτήσειςτέτοιες ώστε
για κάθε
socrates έγραψε:Να προσδιορίσετε όλες τις επί συναρτήσειςτέτοιες ώστε
για κάθε
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες