
Δύσκολη Εκθετική
Συντονιστές: cretanman, silouan, rek2
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Δύσκολη Εκθετική
Μια προσπάθεια...
Χωρίς βλάβη της γενικότητας υποθέτουμε πως .
.
Έχουμε ότι , άρα
, άρα 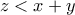
Ακόμα , ενώ
, ενώ 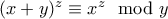 , συνεπώς διακρίνουμε
, συνεπώς διακρίνουμε  περιπτώσεις.
περιπτώσεις.
1) και
και 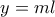 , όπου
, όπου 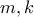 και
και  θετικοί ακέραιοι, αλλά
θετικοί ακέραιοι, αλλά 
Έχουμε:

Όμως , άρα
, άρα  και
και  , που είναι άτοπο, καθώς
, που είναι άτοπο, καθώς 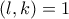
2) , δηλαδή
, δηλαδή  , με
, με  θετικό ακέραιο.
θετικό ακέραιο.
Αντικαθιστώντας και μετά από λίγες πράξεις παίρνουμε ότι: .
.
Επειδή , ισχύει ότι
, ισχύει ότι  , άρα
, άρα 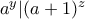 , το οποίο όμως ισχύει μόνο αν
, το οποίο όμως ισχύει μόνο αν  , καθώς
, καθώς  . Συνεπώς
. Συνεπώς  .
.
Αντικαθιστώντας στην αρχική εξίσωση, προκύπτει ότι . Συνεπώς
. Συνεπώς 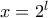 θετικός ακέραιος.
θετικός ακέραιος.
Έχουμε: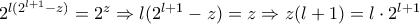 , επομένως
, επομένως  , όπου
, όπου  θετικός ακέραιος, άρα έχουμε πως
θετικός ακέραιος, άρα έχουμε πως  . Συνεπώς
. Συνεπώς  και
και  , όπου
, όπου  και
και  θετικοί ακέραιοι.
θετικοί ακέραιοι.
Έχουμε: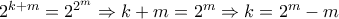 .
.
Δηλαδή
Συνοψίζοντας λύσεις είναι , όπου
, όπου  θετικός ακέραιος
θετικός ακέραιος
edit: Έκανα μια διόρθωση, ελπίζω να είναι σωστή...
Χωρίς βλάβη της γενικότητας υποθέτουμε πως
 .
. Έχουμε ότι
 , άρα
, άρα 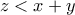
Ακόμα
 , ενώ
, ενώ 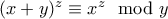 , συνεπώς διακρίνουμε
, συνεπώς διακρίνουμε  περιπτώσεις.
περιπτώσεις.1)
 και
και 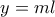 , όπου
, όπου 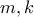 και
και  θετικοί ακέραιοι, αλλά
θετικοί ακέραιοι, αλλά 
Έχουμε:


Όμως
 , άρα
, άρα  και
και  , που είναι άτοπο, καθώς
, που είναι άτοπο, καθώς 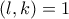
2)
 , δηλαδή
, δηλαδή  , με
, με  θετικό ακέραιο.
θετικό ακέραιο. Αντικαθιστώντας και μετά από λίγες πράξεις παίρνουμε ότι:
 .
. Επειδή
 , ισχύει ότι
, ισχύει ότι  , άρα
, άρα 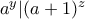 , το οποίο όμως ισχύει μόνο αν
, το οποίο όμως ισχύει μόνο αν  , καθώς
, καθώς  . Συνεπώς
. Συνεπώς  .
. Αντικαθιστώντας στην αρχική εξίσωση, προκύπτει ότι
 . Συνεπώς
. Συνεπώς 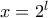 θετικός ακέραιος.
θετικός ακέραιος.Έχουμε:
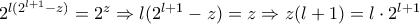 , επομένως
, επομένως  , όπου
, όπου  θετικός ακέραιος, άρα έχουμε πως
θετικός ακέραιος, άρα έχουμε πως  . Συνεπώς
. Συνεπώς  και
και  , όπου
, όπου  και
και  θετικοί ακέραιοι.
θετικοί ακέραιοι.Έχουμε:
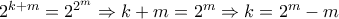 .
.Δηλαδή

Συνοψίζοντας λύσεις είναι
 , όπου
, όπου  θετικός ακέραιος
θετικός ακέραιοςedit: Έκανα μια διόρθωση, ελπίζω να είναι σωστή...
τελευταία επεξεργασία από Διονύσιος Αδαμόπουλος σε Κυρ Δεκ 25, 2016 12:42 pm, έχει επεξεργασθεί 4 φορές συνολικά.
Houston, we have a problem!
Re: Δύσκολη Εκθετική
Μπορεί να κάνω λάθος αλλά το ότι ισχύειΔιονύσιος Αδαμόπουλος έγραψε:Μια προσπάθεια...
....
Ακόμα, ενώ
, συνεπώς
, δηλαδή
, με
θετικό ακέραιο.
 δεν συνεπάγεται απαραίτητα
δεν συνεπάγεται απαραίτητα  . π.χ
. π.χ 
τελευταία επεξεργασία από JimNt. σε Σάβ Δεκ 24, 2016 9:03 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Bye :')
- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Δύσκολη Εκθετική
Χρόνια πολλά και Καλά Χριστούγεννα σε όλα τα μέλη τουJimNt. έγραψε:Μπορεί να κάνω λάθος αλλά το ότι ισχύειΔιονύσιος Αδαμόπουλος έγραψε:Μια προσπάθεια...
....
Ακόμα, ενώ
, συνεπώς
, δηλαδή
, με
θετικό ακέραιο.
δεν συνεπάγεται απαραίτητα
. π.χ
Έκανα μια προσπάθεια να την σώσω, ελπίζω να είναι σωστή...
Houston, we have a problem!
Re: Δύσκολη Εκθετική
Διονύση καλές ΓιορτέςΔιονύσιος Αδαμόπουλος έγραψε:Χρόνια πολλά και Καλά Χριστούγεννα σε όλα τα μέλη τουJimNt. έγραψε:Μπορεί να κάνω λάθος αλλά το ότι ισχύειΔιονύσιος Αδαμόπουλος έγραψε:Μια προσπάθεια...
....
Ακόμα, ενώ
, συνεπώς
, δηλαδή
, με
θετικό ακέραιο.
δεν συνεπάγεται απαραίτητα
. π.χ
!
Έκανα μια προσπάθεια να την σώσω, ελπίζω να είναι σωστή...
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες

 ειναι πρωτος.
ειναι πρωτος.