Αφού με πρόλαβε ο κύριος Γιώργος θα γράψω απλά το γιατί εμφανίζεται το ελάχιστο όταν

.
Αφού

σταθερό έχουμε πως το ελάχιστο του

εμφανίζεται όταν μεγιστοποιείται το

, δηλαδή όταν μεγιστοποιείται η γωνία

.
Ισχύει ότι

, άρα πρέπει να βρούμε πότε μεγιστοποιείται η γωνία

, και αφού

σταθερό πρέπει να μεγιστοποιείται το

.
Είναι γνωστό πως η

είναι η συμμετροδιάμεσος της κορυφής

άρα από γνωστή μετρική σχέση ισχύει ότι

, όπου
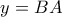
.
Ξέρουμε ταυτόχρονα πως


Ξέρουμε από Πυθαγόρειο πως

, άρα

Θέλουμε λοιπόν να μεγιστοποιείται το
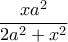
. Όμως έχουμε ότι:

, με ισότητα αν

.
Πράγματι λοιπόν το ελάχιστο του

επιτυγχάνεται όταν

και εύκολα βρίσκουμε πως σε αυτή την περίπτωση είναι

.
 το μήκος της πλευράς
το μήκος της πλευράς  , είναι σταθερό , ενώ της
, είναι σταθερό , ενώ της  μεταβάλλεται .
μεταβάλλεται . , τέμνονται στο σημείο
, τέμνονται στο σημείο  . Η κάθετη της
. Η κάθετη της 
 , τέμνει την προέκταση της
, τέμνει την προέκταση της  στο σημείο
στο σημείο  . Βρείτε το ελάχιστο μήκος του τμήματος
. Βρείτε το ελάχιστο μήκος του τμήματος 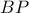 .
.
 μέσο του
μέσο του  Επειδή
Επειδή  είναι συμμετροδιάμεσος θα είναι
είναι συμμετροδιάμεσος θα είναι  οπότε
οπότε  είναι όμοια και:
είναι όμοια και: 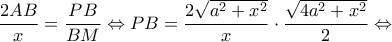
 με
με 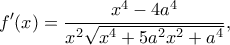 απ' όπου προκύπτει ότι
απ' όπου προκύπτει ότι έχει ελάχιστη τιμή
έχει ελάχιστη τιμή  για
για 
 .
. σταθερό έχουμε πως το ελάχιστο του
σταθερό έχουμε πως το ελάχιστο του  εμφανίζεται όταν μεγιστοποιείται το
εμφανίζεται όταν μεγιστοποιείται το  , δηλαδή όταν μεγιστοποιείται η γωνία
, δηλαδή όταν μεγιστοποιείται η γωνία  .
. , άρα πρέπει να βρούμε πότε μεγιστοποιείται η γωνία
, άρα πρέπει να βρούμε πότε μεγιστοποιείται η γωνία  , και αφού
, και αφού  .
. , όπου
, όπου 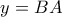 .
.

 , άρα
, άρα 
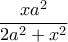 . Όμως έχουμε ότι:
. Όμως έχουμε ότι: , με ισότητα αν
, με ισότητα αν  .
. .
. το μέσο της διαμέτρου
το μέσο της διαμέτρου  . Προφανώς
. Προφανώς  . Θέτω
. Θέτω  .
. τις
τις  .
. . Η
. Η  είναι η συμμετροδιάμεσος στο
είναι η συμμετροδιάμεσος στο 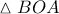 και
και  , θα είναι
, θα είναι 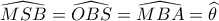 ,
,  είναι εγγράψιμο οπότε εύκολα έχω :
είναι εγγράψιμο οπότε εύκολα έχω :  . Άρα τα
. Άρα τα 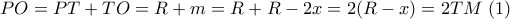
 έχω :
έχω :
 και έτσι οι προηγούμενες δίδουν:
και έτσι οι προηγούμενες δίδουν: με απαλοιφή του
με απαλοιφή του  προκύπτει :
προκύπτει : 
 ,
, 
 έχω :
έχω : .
.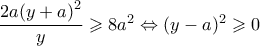 .
.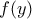 παρουσιάζει ελάχιστο για
παρουσιάζει ελάχιστο για  το
το 