Σελίδα 1 από 1
Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Πέμ Νοέμ 30, 2017 1:17 pm
από silouan
Έστω τρίγωνο

και οι παρεγγεγραμμένοι του κύκλοι
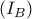
και

. O
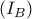
εφάπτεται των

,

στα

αντίστοιχα και ο

των

,

στα
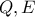
αντίστοιχα. Αν οι
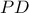
,
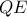
τέμνονται στο

, να αποδειχθεί ότι

.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Παρ Δεκ 01, 2017 5:58 pm
από ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
silouan έγραψε: ↑Πέμ Νοέμ 30, 2017 1:17 pm
Έστω τρίγωνο

και οι παρεγγεγραμμένοι του κύκλοι
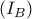
και

. O
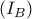
εφάπτεται των

,

στα

αντίστοιχα και ο

των

,

στα
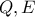
αντίστοιχα. Αν οι
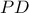
,
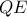
τέμνονται στο

, να αποδειχθεί ότι

.
Εστω
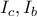
τα κέντρα των
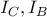
αντίστοιχα.
Από την ομοιότητα των τριγώνων

παίρνουμε

Αν

είναι το ύψος του τριγώνου τότε ο Θαλής μαζί με την προηγούμενη
δίνει
 (1)
(1)
Εστω

Εύκολα βλέπουμε ότι τα τρίγωνα

είναι όμοια.
Ετσι έχουμε

Αλλά
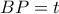
όπου

η ημιπερίμετρος.
Αρα
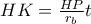 (2)
(2)
Αν τώρα

υπολογίζουμε όμοια ότι
 (3)
(3)
Τελικά οι (1), (2), (3) μας δίνουν ότι

και το ζητούμενο απεδείχθη.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Σάβ Δεκ 02, 2017 1:07 am
από Διονύσιος Αδαμόπουλος
silouan έγραψε: ↑Πέμ Νοέμ 30, 2017 1:17 pm
Έστω τρίγωνο

και οι παρεγγεγραμμένοι του κύκλοι
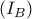
και

. O
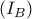
εφάπτεται των

,

στα

αντίστοιχα και ο

των

,

στα
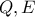
αντίστοιχα. Αν οι
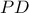
,
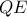
τέμνονται στο

, να αποδειχθεί ότι

.
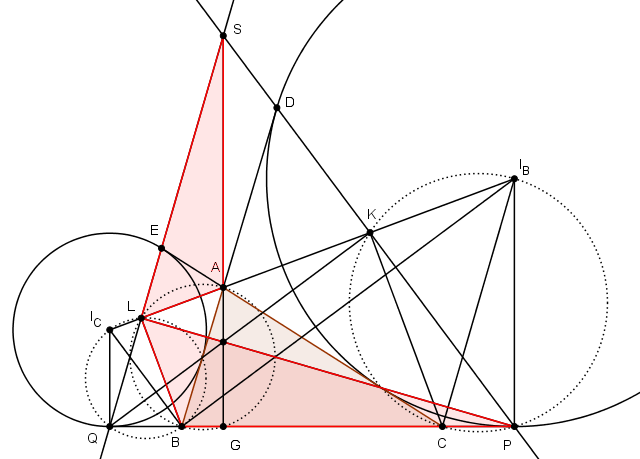
- Καθετότητα με δύο παρεγγεγραμμένους (2).png (43 KiB) Προβλήθηκε 1625 φορές
Έστω πως οι
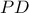
και
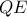
τέμνουν την εξωτερική διχοτόμο της γωνίας

του τριγώνου

, η οποία είναι και διάκεντρος των κύκλων

, στα σημεία

. Ακόμα έστω πως η

τέμνει την

στο

.
Παρατηρούμε πως

Όμως είναι

, άρα αφού
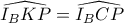
, προκύπτει ότι

είναι εγγράψιμο.
Επομένως αφού
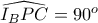
, προκύπτει ότι
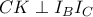
.
Ομοίως προκύπτει ότι
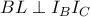
.
Έχουμε πως

Παρατηρούμε πως το τετράπλευρο

είναι εγγράψιμο. Ακόμη ξέρουμε πως

, άρα προκύπτει πως

.
Συνεπώς είναι

, άρα είναι
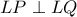
.
Ακόμη έχουμε πως

(1)
Επιπλέον τα ορθογώνια τρίγωνα

και
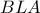
είναι όμοια αφού


.
Επομένως

(2)
Από τις σχέσεις (1) και (2) προκύπτει ότι τα τρίγωνα

και
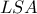
είναι όμοια, άρα

, επομένως το τετράπλευρο
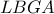
είναι εγγράψιμο και αφού

προκύπτει ότι

.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Τετ Δεκ 06, 2017 12:51 am
από silouan
Πολύ ωραίες οι λύσεις σας! Πριν παραθέσω την δική μου, να ρωτήσω: Υπάρχει σύντομη λύση στο παραπάνω πρόβλημα με το Θεώρημα Κούτρα;
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 8:14 pm
από vittasko
Χρησιμοποιώ προς το παρόν, το σχήμα του Διονύση πιο πάνω ( 3η δημοσίευση ).

Έστω τα σημεία
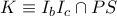
και
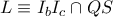
.
Στο ορθογώνιο τραπέζιο

, από

, σύμφωνα με το γνωστό Λήμμα που είδαμε πρόσφατα
Εδώ, προκύπτει ότι

Από

και


και ομοίως, έχουμε

Από

προκύπτει ότι το σημείο έστω

ταυτίζεται με το ορθόκεντρο του τριγώνου

και επομένως, ισχύει


Έστω το σημείο

και από το πλήρες τετράπλευρο

έχουμε ότι η σημειοσειρά
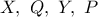
είναι αρμονική, όπου

( αντί του σημείου

στο σχήμα ).
Από την αρμονικότητα της ως άνω σημειοσειράς, προκύπτει ότι
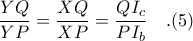
λόγω
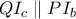
.
Από τα όμοια ορθογώνια τρίγωνα

έχουμε
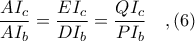
Από
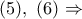
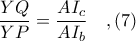
Από


και άρα, ισχύει

Από



και το ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 9:14 pm
από S.E.Louridas
Γεια χαρά.
Έστω

η επαφή του κύκλου

με την

και
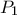
η επαφή του κύκλου

με την

Τότε προφανώς έχουμε
 (*)
(*)
οπότε το σημείο τομής

των

θα είναι το ορθόκεντρο του τριγώνου
Ταυτόχρονα έχουμεQ

Άρα τα σημεία
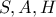
είναι συνευθειακά.
(*) Επειδή οι
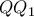
,

είναι παράλληλες στις διχοτόμους των γωνιών
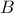
και

αντίστοιχα.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 9:20 pm
από min##
Αλλιώς:Αν

το έκκεντρο και η προβολή του στην

και

οι προβολές του

στις

,λόγω του εγγράψιμου

(απλό),θα είναι τα

όμοια.Είναι

,δηλαδή

και

,δηλαδή
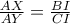
και επειδή

τα

είναι όμοια,δηλαδή και τα
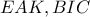
είναι (αντιστρόφως) όμοια,άρα είναι και ορθολογικά κλπ.
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 10:38 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 10:53 pm
από min##
Με την παραπάνω σχέση για το

και 2 Μενέλαους στα
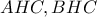
με διατέμνουσες τις

,αρκεί

,δηλαδή
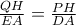
το οποίο τσεκάρεται απλούστατα.(

το οποίο και λόγω κυκλικότητας των

είναι ίσο με

)
Re: Καθετότητα με δύο παρεγγεγραμμένους
Δημοσιεύτηκε: Κυρ Οκτ 28, 2018 11:11 pm
από ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 και οι παρεγγεγραμμένοι του κύκλοι
και οι παρεγγεγραμμένοι του κύκλοι  και
και  . O
. O 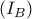 εφάπτεται των
εφάπτεται των  ,
,  στα
στα  αντίστοιχα και ο
αντίστοιχα και ο  των
των  ,
,  στα
στα 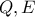 αντίστοιχα. Αν οι
αντίστοιχα. Αν οι 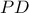 ,
, 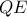 τέμνονται στο
τέμνονται στο  , να αποδειχθεί ότι
, να αποδειχθεί ότι  .
. και οι παρεγγεγραμμένοι του κύκλοι
και οι παρεγγεγραμμένοι του κύκλοι 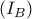 και
και  . O
. O 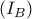 εφάπτεται των
εφάπτεται των  ,
,  στα
στα  αντίστοιχα και ο
αντίστοιχα και ο  των
των  ,
,  στα
στα 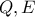 αντίστοιχα. Αν οι
αντίστοιχα. Αν οι 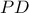 ,
, 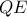 τέμνονται στο
τέμνονται στο  , να αποδειχθεί ότι
, να αποδειχθεί ότι  .
.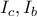 τα κέντρα των
τα κέντρα των 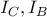 αντίστοιχα.
αντίστοιχα.

 είναι το ύψος του τριγώνου τότε ο Θαλής μαζί με την προηγούμενη
είναι το ύψος του τριγώνου τότε ο Θαλής μαζί με την προηγούμενη 



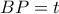 όπου
όπου  η ημιπερίμετρος.
η ημιπερίμετρος.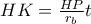



 του τριγώνου
του τριγώνου  , στα σημεία
, στα σημεία  . Ακόμα έστω πως η
. Ακόμα έστω πως η  τέμνει την
τέμνει την  .
.
 , άρα αφού
, άρα αφού 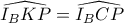 , προκύπτει ότι
, προκύπτει ότι  είναι εγγράψιμο.
είναι εγγράψιμο. 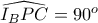 , προκύπτει ότι
, προκύπτει ότι 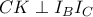 .
.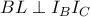 .
.
 είναι εγγράψιμο. Ακόμη ξέρουμε πως
είναι εγγράψιμο. Ακόμη ξέρουμε πως  , άρα προκύπτει πως
, άρα προκύπτει πως  .
. , άρα είναι
, άρα είναι 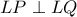 .
. (1)
(1) και
και 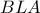 είναι όμοια αφού
είναι όμοια αφού 
 .
. (2)
(2) και
και 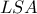 είναι όμοια, άρα
είναι όμοια, άρα  , επομένως το τετράπλευρο
, επομένως το τετράπλευρο 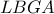 είναι εγγράψιμο και αφού
είναι εγγράψιμο και αφού  προκύπτει ότι
προκύπτει ότι  .
. Έστω τα σημεία
Έστω τα σημεία 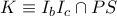 και
και 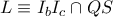 .
. , από
, από  , σύμφωνα με το γνωστό Λήμμα που είδαμε πρόσφατα
, σύμφωνα με το γνωστό Λήμμα που είδαμε πρόσφατα 
 και
και 
 και ομοίως, έχουμε
και ομοίως, έχουμε 
 προκύπτει ότι το σημείο έστω
προκύπτει ότι το σημείο έστω  ταυτίζεται με το ορθόκεντρο του τριγώνου
ταυτίζεται με το ορθόκεντρο του τριγώνου 

 και από το πλήρες τετράπλευρο
και από το πλήρες τετράπλευρο 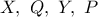 είναι αρμονική, όπου
είναι αρμονική, όπου  ( αντί του σημείου
( αντί του σημείου 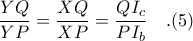 λόγω
λόγω 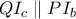 .
. έχουμε
έχουμε 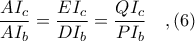
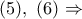
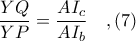

 και άρα, ισχύει
και άρα, ισχύει 


 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. η επαφή του κύκλου
η επαφή του κύκλου  με την
με την 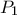 η επαφή του κύκλου
η επαφή του κύκλου  με την
με την  Τότε προφανώς έχουμε
Τότε προφανώς έχουμε 
 των
των  θα είναι το ορθόκεντρο του τριγώνου
θα είναι το ορθόκεντρο του τριγώνου 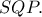

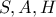 είναι συνευθειακά.
είναι συνευθειακά.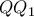 ,
,  είναι παράλληλες στις διχοτόμους των γωνιών
είναι παράλληλες στις διχοτόμους των γωνιών 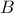 και
και  αντίστοιχα.
αντίστοιχα. το έκκεντρο και η προβολή του στην
το έκκεντρο και η προβολή του στην  οι προβολές του
οι προβολές του  ,λόγω του εγγράψιμου
,λόγω του εγγράψιμου  (απλό),θα είναι τα
(απλό),θα είναι τα  όμοια.Είναι
όμοια.Είναι  ,δηλαδή
,δηλαδή  και
και  ,δηλαδή
,δηλαδή 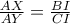 και επειδή
και επειδή  τα
τα  είναι όμοια,δηλαδή και τα
είναι όμοια,δηλαδή και τα 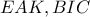 είναι (αντιστρόφως) όμοια,άρα είναι και ορθολογικά κλπ.
είναι (αντιστρόφως) όμοια,άρα είναι και ορθολογικά κλπ. Με
Με 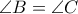 η πρόταση είναι προφανής (λόγω συμμετρίας του σχήματος ως προς την μεσοκάθετη της
η πρόταση είναι προφανής (λόγω συμμετρίας του σχήματος ως προς την μεσοκάθετη της 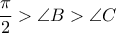 και ας είναι
και ας είναι  οι ορθές προβολές του
οι ορθές προβολές του  (το
(το  παράκεντρο) στην
παράκεντρο) στην  και
και  (παράλληλες πλευρές) για τις ομόλογες πλευρές και προβολές θα ισχύει:
(παράλληλες πλευρές) για τις ομόλογες πλευρές και προβολές θα ισχύει: 
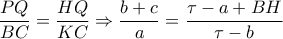




 και το ζητούμενο έχει αποδειχθεί
και το ζητούμενο έχει αποδειχθεί 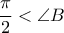

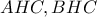 με διατέμνουσες τις
με διατέμνουσες τις  ,αρκεί
,αρκεί ,δηλαδή
,δηλαδή 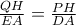 το οποίο τσεκάρεται απλούστατα.(
το οποίο τσεκάρεται απλούστατα.( το οποίο και λόγω κυκλικότητας των
το οποίο και λόγω κυκλικότητας των  είναι ίσο με
είναι ίσο με  )
) και ας είναι
και ας είναι  το σημείο επαφής του
το σημείο επαφής του  είναι παραλληλόγραμμο (απέναντι πλευρές κάθετες στην ίδια ευθεία) οπότε οι διαγώνιες διχοτομούνται.
είναι παραλληλόγραμμο (απέναντι πλευρές κάθετες στην ίδια ευθεία) οπότε οι διαγώνιες διχοτομούνται.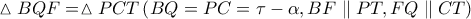
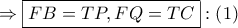

 και
και 

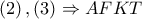 παραλληλόγραμμο. Από τα παραλληλόγραμμα
παραλληλόγραμμο. Από τα παραλληλόγραμμα  που μοιράζονται την διαγώνιο
που μοιράζονται την διαγώνιο  προκύπτει ότι και
προκύπτει ότι και  είναι παραλληλόγραμμο (οι διαγώνιες διχοτομούνται) οπότε
είναι παραλληλόγραμμο (οι διαγώνιες διχοτομούνται) οπότε 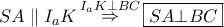 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.