Εμβαδόν εγγεγραμμένου τριγώνου

#1

: Εμβαδόν εγγεγραμμένου τριγώνου.png (15.67 KiB) Προβλήθηκε 1422 φορές

Τρίγωνο

του οποίου οι πλευρές AB, AC, BC

είναι διαδοχικοί όροι αριθμητικής προόδου, είναι περιγεγραμμένο σε κύκλο

ακτίνας

και έστω

τα σημεία επαφής του κύκλου με τις BC, AC, AB

αντίστοιχα. Αν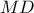

είναι το ύψος και

το

ορθόκεντρο του τριγώνου KLM

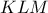και

να υπολογίσετε το εμβαδόν του KLM

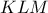συναρτήσει του

ΚΕΦΑΛΟΝΙΤΗΣ · #2

Το θέμα το αντιμετώπισα με αρκετή τριγωνομετρία. Ίσως υπάρχει πιο κομψή λύση...

Όποιος έχει βασικές γεωμετρικές γνώσεις βρίσκει ότι

$\displaystyle K\hat{M}L=90^{o}-\frac{C}{2}$

$\displaystyle K\hat{L}M=90^{o}-\frac{B}{2}$

$\displaystyle M\hat{K}L =90^{o}-\frac{A}{2}$

Από την Τριγωνομετρία γνωρίζουμε ότι ισχύει $\displaystyle MH=2r\cdot cosK\hat{M}L=2r\cdot cos\left ( 90^{o}-\frac{C}{2} \right )=2r\cdot sin\frac{C}{2}$

και επίσης ότι

$\displaystyle HD=2r\cdot cosK\hat{L}M \cdot cosM\hat{K}L =2r\cdot cos\left ( 90^{o}-\frac{B}{2} \right ) \cdot cos\left ( 90^{o}-\frac{A}{2} \right ) =2r\cdot sin\frac{B}{2}\cdot sin\frac{A}{2}$

Σύμφωνα με τα δεδομένα

$\displaystyle HD=MH\Leftrightarrow HD^{2}=MH^{2}\Leftrightarrow sin^{2}\frac{C}{2}=sin^{2}\frac{A}{2}\cdot sin^{2}\frac{B}{2}$

το οποίο ισοδυναμεί με

$\displaystyle \frac{\left ( s-a \right )\left ( s-b \right )}{ab}=\frac{\left ( s-a \right )\left ( s-c \right )}{ac}\cdot \frac{\left ( s-b \right )\left ( s-c \right )}{bc}$

και αυτό είναι ισοδύναμο με

$\left ( s-c \right )^{2}=c^{2}\Leftrightarrow s-c=c\Leftrightarrow s=2c$

Oι πλευρές c,b,a

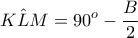
αποτελούν διαδοχικούς όρους αριθμητικής προόδου , άρα

$\displaystyle s=\frac{a+b+c}{2}=\frac{3b}{2}$

Συνεπώς $\displaystyle \frac{3b}{2}=2c\Rightarrow c=\frac{3b}{4}$

Έτσι η διαφορά της προόδου είναι ίση με

$\displaystyle b-c=b-\frac{3b}{4}=\frac{b}{4}$

Έυκολα πλέον βρίσκεται ότι

$\displaystyle a=b+\frac{3b}{4}=\frac{5b}{4}$

Συνεπώς

$\displaystyle s-a=\frac{3b}{2}-\frac{5b}{4}=\frac{b}{4}$

$\displaystyle s-b=\frac{3b}{2}-b=\frac{b}{2}$

$\displaystyle s-c=\frac{3b}{2}-\frac{3b}{4}=\frac{3b}{4}$

Aπό την Τριγωνομετρία γνωρίζουμε ότι

$\displaystyle \left ( KLM \right )=2r^{2} \cdot sin K\hat{M}L\cdot sin K\hat{L}M\cdot sin M\hat{K}L=$

$\displaystyle 2r^{2}\cdot sin\left ( 90^{0}-\frac{A}{2} \right )\cdot sin\left ( 90^{0}-\frac{B}{2} \right )\cdot sin \left ( 90^{0}-\frac{C}{2} \right )=$

$\displaystyle 2r^{2} \cdot cos\frac{A}{2}\cdot cos\frac{B}{2} \cdot cos\frac{C}{2}$

Όμως

$\displaystyle cos\frac{A}{2}=\sqrt{\frac{s \left ( s-a \right )}{bc}}=\sqrt{\frac{\frac{3b}{2}\cdot \frac{b}{4}}{b\cdot \frac{3b}{4}}}=\sqrt{\frac{1}{2}}$

$\displaystyle cos\frac{B}{2}=\sqrt{\frac{s \left ( s-b \right )}{ac}}=\sqrt{\frac{\frac{3b}{2}\cdot \frac{b}{2}}{ \frac{5b}{4}\cdot \frac{3b}{4}}}=\sqrt{\frac{4}{5}}$

$\displaystyle cos\frac{C}{2}=\sqrt{\frac{s \left ( s-c \right )}{ab}}=\sqrt{\frac{\frac{3b}{2}\cdot \frac{3b}{4}}{ \frac{5b}{4}\cdot b}}=\sqrt{\frac{9}{10}}$

Έτσι λοιπόν

$\displaystyle \left ( KLM \right )=2r^{2}\sqrt{\frac{1}{2}}\cdot\sqrt{\frac{4}{5}}\cdot \sqrt{\frac{9}{10}}=2r^{2}\sqrt{\frac{9}{25}}=2r^{2}\cdot\frac{3}{5}=\frac{6}{5}} \cdot r^{2}$

Η λύση ίσως δεν είναι πολύ κομψή. Περιμένω τις σκέψεις σας...
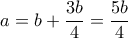
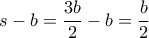
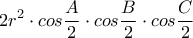
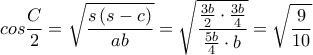
Πάντως από τα παραπάνω προκύπτει ότι η γωνία οφείλει να είναι ορθή...
Επίσης προκύπτει ότι τα άπειρα τρίγωνα που ικανοποιούν τα δεδομένα του θέματος είναι όμοια μεταξύ τους.

#3

Να ευχαριστήσω τον Τηλέμαχο για την ωραία λύση του, που ανέδειξε τις αρετές της Τριγωνομετρίας.
Θα συνεχίσω λίγο διαφορετικά από το σημείο που ο Τηλέμαχος βρήκε $c=\dfrac{3b}{4}, a=\dfrac{5b}{4}$

: Εμβαδόν εγγεγραμμένου τριγώνου.b.png (18.45 KiB) Προβλήθηκε 1245 φορές

Παρατηρούμε ότι το τρίγωνο ABC

είναι ορθογώνιο με πλευρές (3k, 4k, 5k)

και άρα

οπότε προκύπτουν τα μήκη των τμημάτων που φαίνονται στο σχήμα και ως εκ τούτου $\displaystyle \sin B = \frac{4}{5},\sin C = \frac{3}{5}$ .

$\displaystyle (KLM) = (ABC) - (AML) - (BMK) - (CLK)$

$\displaystyle (KLM) = 6{r^2} - \frac{{{r^2}}}{2} - \frac{1}{2}4{r^2}\sin B - \frac{1}{2}9{r^2}\sin C \Leftrightarrow$ $\boxed{KLM)=\frac{6r^2}{5}}$

ΥΓ: Η άσκηση είναι από PUMAC 2015 (6ο πρόβλημα) με κάποια παραλλαγή, αλλά η λύση που έχει στο συνημμένο είναι αρκετά πολύπλοκη και δεν με ικανοποιεί.

Εμβαδόν εγγεγραμμένου τριγώνου

Εμβαδόν εγγεγραμμένου τριγώνου

Re: Εμβαδόν εγγεγραμμένου τριγώνου

Re: Εμβαδόν εγγεγραμμένου τριγώνου

Μέλη σε σύνδεση