Διπλωμένο τετράγωνο

#1

: Διπλωμένο τετράγωνο.png (11.67 KiB) Προβλήθηκε 987 φορές

Η πλευρά

τετραγώνου ABCD

διπλώνεται όπως φαίνεται στο σχήμα και παίρνει τη νέα θέση LS.

Έστω

ο έγκυκλος του τριγώνου CST.

α) Να δείξετε ότι LT=r

β) Να βρείτε τη μέγιστη τιμή της ακτίνας

καθώς και τη θέση του

για την οποία επιτυγχάνεται.

#2

george visvikis έγραψε:Διπλωμένο τετράγωνο.png
Η πλευρά τετραγώνου διπλώνεται όπως φαίνεται στο σχήμα και παίρνει τη νέα θέση Έστω ο έγκυκλος του τριγώνου
α) Να δείξετε ότι
β) Να βρείτε τη μέγιστη τιμή της ακτίνας καθώς και τη θέση του για την οποία επιτυγχάνεται.

Καλημέρα Γιώργο και Χρόνια σου πολλά, καλά και δημιουργικά!!!

$\bullet$ Προφανώς 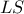το συμμετρικό του ως προς την και άρα αν το σημείο τομής της εκ του καθέτου στον άξονα συμμετρίας τότε (από τη συμμετρία) θα ισχύει: $\boxed{TL = DE}:\left( 1 \right)$ .

Από τη συμμετρία το τετράπλευρο είναι ισοσκελές τραπέζιο άρα τα σημεία είναι ομοκυκλικά.

Από τη συμμετρία προκύπτει ότι $\angle TSP = \angle EAP = {90^0} \Rightarrow \boxed{\angle SPB\mathop = \limits^{o\xi \varepsilon \iota \varepsilon \varsigma \;\mu \varepsilon \;\kappa \alpha \theta \varepsilon \tau \varepsilon \varsigma \;\pi \lambda \varepsilon \upsilon \rho \varepsilon \varsigma } \angle TSC}:\left( 2 \right)$ .

Από $\left( 1 \right) \Rightarrow 2\left( {\angle SPA} \right)\mathop = \limits^{PS = PA\left( {\sigma \upsilon \mu \mu \varepsilon \tau \rho \iota \alpha } \right),SK\;\delta \iota \chi o\tau o\mu o\varsigma \;\tau \eta \varsigma \;\angle TSC} 2\left( {\angle KST} \right)$ $\Rightarrow \angle SPA = \angle KST\mathop \Rightarrow \limits^{SK\;\delta \iota \chi o\tau o\mu o\varsigma \;\tau o\upsilon \;\vartriangle SMC\left( {M \equiv AC \cap ST} \right)} SA$

η εξωτερική διχοτόμος του $\vartriangle SCM$ και άρα σειρά $\left( C,K,M,A \right)$ είναι αρμονική οπότε και η δέσμη είναι αρμονική και με διχοτόμο της

$\angle CTM \Rightarrow TA \bot TK \Rightarrow$ $\angle KTA = {90^0} = \angle KSA \Rightarrow A,S,K,T$ ομοκυκλικά.
[attachment=1]Διπλωμένο τετράγωνο.png[/attachment]
$\bullet$ Από τις ομοκυκλικές τετράδες $\left( A,E,T,S \right)$ και $\left( A,S,K,T \right)$ με τρία κοινά σημεία $A,S,T\Rightarrow A,E,S,K,T$ είναι σημεία κύκλου διαμέτρου

$AK \Rightarrow \angle AEK = {90^0} \Rightarrow KE \bot AD\mathop \Rightarrow \limits^{CD \bot AD}$ $KE\parallel CD\mathop \Rightarrow \limits^{DE \bot DC,KZ \bot AD} DE = KZ = r\mathop \Rightarrow \limits^{\left( 1 \right)} \boxed{TL = r}$

και το α) ζητούμενο έχει αποδειχθεί.

Από την $\left( 1 \right)\mathop \Rightarrow \limits^{\angle PBS = \angle SCT = {{90}^0}} \boxed{\vartriangle PBS = \vartriangle SCT}:\left( 3 \right)$

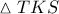$\bullet$ Στο τρίγωνο $\vartriangle TKS$ για το ύψους του και τη σεβιανή του 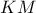ισχύει: $r=KF\le KM$ με τη μέγιστη τιμή της να πραγματοποιηθεί

αν $KF = KM \Rightarrow KM \bot TS\mathop \Rightarrow \limits^{K,M,C\;\sigma \upsilon \nu \varepsilon \upsilon \theta \varepsilon \iota \alpha \kappa \alpha }$ $CM \bot TS\mathop \Rightarrow \limits^{TKM\;\delta \iota \chi o\tau o\mu o\varsigma \;\tau \eta \varsigma \;\angle TCS} \vartriangle TCS$

ορθογώνιο ισοσκελές (το ύψος του από την κορυφή της ορθής γωνίας ταυτίζεται με την αντίστοιχη διχοτόμο)

οπότε από την $\left( 3 \right)\Rightarrow \vartriangle PBS$ ορθογώνιο ισοσκελές οπότε $\angle SPB = {45^0}\mathop \Rightarrow \limits^{PS = PA} \angle PAS = {22,5^0} = \dfrac{{{{45}^0}}}{2} = \dfrac{{\angle BAC}}{2}$

άρα η μεγιστοποίηση της ακτίνας θα προκύψει αν είναι το σημείο τομής της διχοτόμου της γωνίας $\angle BAC$ με την .
[attachment=0]Διπλωμένο τετράγωνο.png[/attachment]
Τότε με $\angle CSK = {22,5^0} = \angle SAC \Rightarrow CS = AP$ εφαπτόμενη του κύκλου

$\left( {A,S,K,T,E} \right) \Rightarrow CK \cdot CA = C{S^2} = A{P^2} \Rightarrow$ $r\sqrt 2 \cdot a\sqrt 2 = A{P^2} \Rightarrow \boxed{{r_{\max }} = \dfrac{{A{P^2}}}{{2a}}}:\left( 4 \right)$ .

Αλλά $AP = a - PB = a - \dfrac{{PS}}{{\sqrt 2 }} = a - \dfrac{{AP}}{{\sqrt 2 }} \Rightarrow$ $\ldots AP = \dfrac{{a\sqrt 2 }}{{\sqrt 2 + 1}}\mathop \Rightarrow \limits^{\left( 4 \right)}$ ${r_{\max }} = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{{\sqrt 2 + 1}}} \right)}^2}}}{{2a}} \Rightarrow \ldots \boxed{{r_{\max }} = a\left( {3 - 2\sqrt 2 } \right)}$

και το β) ζητούμενο έχει βρεθεί και υπολογιστεί.

Στάθης

KARKAR · #3

Μια σχετική ανάρτηση είναι αυτή

harrisp · #4

george visvikis έγραψε:Διπλωμένο τετράγωνο.png
Η πλευρά τετραγώνου διπλώνεται όπως φαίνεται στο σχήμα και παίρνει τη νέα θέση Έστω ο έγκυκλος του τριγώνου

α) Να δείξετε ότι

β) Να βρείτε τη μέγιστη τιμή της ακτίνας καθώς και τη θέση του για την οποία επιτυγχάνεται.

Ας αποδειχτεί και το εξής:

Έστω r_1

η ακτίνα του εγκύκλου του τριγώνου LQT

και

του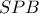

. Να δειχτεί:

$\boxed {r=r_1+r_2}$

ΥΓ. Δεν έχω δεί ούτε την παραπομπή ούτε και την λύση του κύριου Στάθη λόγω ελλιπούς χρονικού περιθωρίου. Ελπίζω να μην αναφέρεται.

Διπλωμένο τετράγωνο

Διπλωμένο τετράγωνο

Re: Διπλωμένο τετράγωνο

Re: Διπλωμένο τετράγωνο

Re: Διπλωμένο τετράγωνο

Μέλη σε σύνδεση