 ενός κύκλου
ενός κύκλου  φέρνω το εφαπτόμενο τμήμα
φέρνω το εφαπτόμενο τμήμα  και μία τέμνουσα
και μία τέμνουσα  Να βρεθεί η γωνία
Να βρεθεί η γωνία  για την οποία μεγιστοποιείται το εμβαδόν
για την οποία μεγιστοποιείται το εμβαδόν 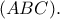
 ενός κύκλου
ενός κύκλου  φέρνω το εφαπτόμενο τμήμα
φέρνω το εφαπτόμενο τμήμα  και μία τέμνουσα
και μία τέμνουσα  Να βρεθεί η γωνία
Να βρεθεί η γωνία  για την οποία μεγιστοποιείται το εμβαδόν
για την οποία μεγιστοποιείται το εμβαδόν 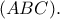
Με αρχή αξόνων τοgeorge visvikis έγραψε:Γωνία μεγιστοποίησης εμβαδού.png
Σε σημείοενός κύκλου
φέρνω το εφαπτόμενο τμήμα
και μία τέμνουσα
Να βρεθεί η γωνία
για την οποία μεγιστοποιείται το εμβαδόν
 και μοναδιαίο διάνυσμα
και μοναδιαίο διάνυσμα  θα έχω τις εξισώσεις:
θα έχω τις εξισώσεις:  και της ευθείας ,
και της ευθείας , 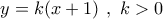 .
.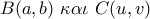 :
: και έτσι
και έτσι 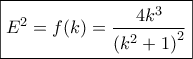
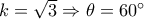 με
με ![\boxed{{E_{\max }} = \frac{{\sqrt[4]{{108}}}}{4}} \boxed{{E_{\max }} = \frac{{\sqrt[4]{{108}}}}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/8692d0b74ea5308555bcdd9c9af13757.png) .
.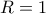 και θέτω
και θέτω  οπότε
οπότε 
 και με νόμο συνημιτόνων έχω:
και με νόμο συνημιτόνων έχω: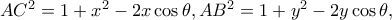 και από την
και από την  είναι
είναι 
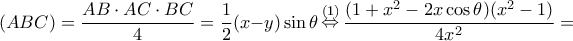

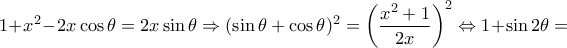




 παρουσιάζει για
παρουσιάζει για 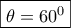 μέγιστη τιμή ίση με
μέγιστη τιμή ίση με ![\boxed{{(ABC)_{\max }} = \frac{{\sqrt[4]{{108}}}}{4}} \boxed{{(ABC)_{\max }} = \frac{{\sqrt[4]{{108}}}}{4}}](/forum/ext/geomar/texintegr/latexrender/pictures/ab5590347f83300821fca72587d82705.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες