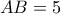 , γράψτε κύκλο ακτίνας
, γράψτε κύκλο ακτίνας  ,
,εφαπτόμενο σε ημικύκλιο και διάμετρο . Υπολογίστε στη συνέχεια
τον λόγο :
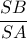 ( θέλουμε αποτέλεσμα χωρίς κλάσματα και ρίζες ) .
( θέλουμε αποτέλεσμα χωρίς κλάσματα και ρίζες ) .Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
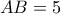 , γράψτε κύκλο ακτίνας
, γράψτε κύκλο ακτίνας  ,
,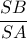 ( θέλουμε αποτέλεσμα χωρίς κλάσματα και ρίζες ) .
( θέλουμε αποτέλεσμα χωρίς κλάσματα και ρίζες ) .α) Με Πυθαγόρειο βρίσκω
 Στο σημείο
Στο σημείο  λοιπόν, υψώνω κάθετο στη διάμετρο και παίρνω τμήμα
λοιπόν, υψώνω κάθετο στη διάμετρο και παίρνω τμήμα 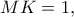 οπότε εντοπίζω το κέντρο του κύκλου.
οπότε εντοπίζω το κέντρο του κύκλου.


 τα κέντρα του μεγάλου και μικρού κύκλου και
τα κέντρα του μεγάλου και μικρού κύκλου και  το σημείο επαφής του μικρού με την
το σημείο επαφής του μικρού με την  .
. που τέμνει την ευθεία
που τέμνει την ευθεία  στο σημείο
στο σημείο  .
. είναι ίσα θα έχω
είναι ίσα θα έχω  . Αλλά η
. Αλλά η  είναι εξωτερική στο
είναι εξωτερική στο  και άρα,
και άρα, 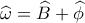 .
.  λόγω χορδής κι εφαπτομένης θα έχω :
λόγω χορδής κι εφαπτομένης θα έχω :  .
.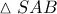 θα είναι :
θα είναι :
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες