 . Προεκτείνουμε τις
. Προεκτείνουμε τις  κατά τμήματα
κατά τμήματα 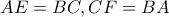 αντίστοιχα. Να αποδειξετε ότι
αντίστοιχα. Να αποδειξετε ότι 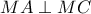 , όπου
, όπου  το μέσο της
το μέσο της  .
.Μέχρι τον νέο μήνα για μαθητές.
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 . Προεκτείνουμε τις
. Προεκτείνουμε τις  κατά τμήματα
κατά τμήματα 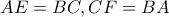 αντίστοιχα. Να αποδειξετε ότι
αντίστοιχα. Να αποδειξετε ότι 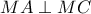 , όπου
, όπου  το μέσο της
το μέσο της  .
. βρίσκεται στο διαφορετικό ημιεπίπεδο από το
βρίσκεται στο διαφορετικό ημιεπίπεδο από το  ως προς την
ως προς την  .
. και
και  τα συμμετρικά του
τα συμμετρικά του  και του
και του  προς τα
προς τα  και
και  αντίστοιχα. Έστω
αντίστοιχα. Έστω 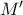 το μέσο του
το μέσο του  .
. τα
τα  είναι τα μέσα των πλευρών, επομένως το
είναι τα μέσα των πλευρών, επομένως το  είναι παραλληλόγραμμο. Με άλλα λόγια είναι
είναι παραλληλόγραμμο. Με άλλα λόγια είναι  και
και  (*) και
(*) και  (1).
(1). και
και  (2).
(2). .
. λόγω του εγγραψίμου.
λόγω του εγγραψίμου.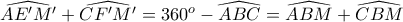 (3)
(3) ) και (
) και ( ) αποτελούν ζευγάρια ίσων τριγώνων (αν δεν είναι τα τρίγωνα του ενός ζευγαριού ίσα, τότε δεν είναι και στο άλλο καθώς θα ήταν
) αποτελούν ζευγάρια ίσων τριγώνων (αν δεν είναι τα τρίγωνα του ενός ζευγαριού ίσα, τότε δεν είναι και στο άλλο καθώς θα ήταν  ).
). έτσι ώστε
έτσι ώστε  και
και  και
και  (αυτό μπορούμε να το κάνουμε σύμφωνα με τη σχέση (3)) και το
(αυτό μπορούμε να το κάνουμε σύμφωνα με τη σχέση (3)) και το  να είναι στο άλλο ημιεπίπεδο από το
να είναι στο άλλο ημιεπίπεδο από το  ως προς την
ως προς την  .
. και
και  αποτελούν ζευγάρια ίσων τριγώνων.
αποτελούν ζευγάρια ίσων τριγώνων. και
και  .
.  και
και 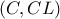 . Αυτοί σύμφωνα με την παραπάνω σχέση τέμνονται στο
. Αυτοί σύμφωνα με την παραπάνω σχέση τέμνονται στο  και στο
και στο  . Όμως αφού και το
. Όμως αφού και το  και το
και το  ανήκουν στο ίδιο ημιεπίπεδο ως προς την
ανήκουν στο ίδιο ημιεπίπεδο ως προς την  έχουμε άτοπο.
έχουμε άτοπο. .
. και
και  αποτελούν ζευγάρια ίσων τριγώνων.
αποτελούν ζευγάρια ίσων τριγώνων.
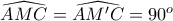 .
.Ευχαριστώ για την λύση Διονύση. Νομίζω πως φτάνουμε πιο εύκολα στην λύση θεωρώντας το συμμετρικό τουΔιονύσιος Αδαμόπουλος έγραψε: ↑Δευ Φεβ 26, 2018 11:03 pmΚαθετότητα στο Μέσο.png
Καταρχάς είναι προφανές πως τοβρίσκεται στο διαφορετικό ημιεπίπεδο από το
ως προς την
.
Έστωκαι
τα συμμετρικά του
και του
προς τα
και
αντίστοιχα. Έστω
το μέσο του
.
Παρατηρούμε πως στο τετράπλευροτα
είναι τα μέσα των πλευρών, επομένως το
είναι παραλληλόγραμμο. Με άλλα λόγια είναι
και
(*) και
(1).
Ταυτόχρονα είναικαι
(2).
Ακόμη ξέρουμε πως.
Ξέρουμε παρόλα αυτά πωςλόγω του εγγραψίμου.
Συνεπώς είναι(3)
Θέλουμε να αποδείξουμε πως τα τρίγωνα () και (
) αποτελούν ζευγάρια ίσων τριγώνων (αν δεν είναι τα τρίγωνα του ενός ζευγαριού ίσα, τότε δεν είναι και στο άλλο καθώς θα ήταν
).
Πράγματι έστω πως αυτά δεν είναι ίσα.
Επιλέγουμε ένα σημείοέτσι ώστε
και
και
(αυτό μπορούμε να το κάνουμε σύμφωνα με τη σχέση (3)) και το
να είναι στο άλλο ημιεπίπεδο από το
ως προς την
.
Τώρα σε συνδυασμό με τη σχέση (2) παίρνουμε πως τα τρίγωνακαι
αποτελούν ζευγάρια ίσων τριγώνων.
Επομένως χρησιμοποιώντας και την (*) είναικαι
.
Θεωρούμε τους κύκλουςκαι
. Αυτοί σύμφωνα με την παραπάνω σχέση τέμνονται στο
και στο
. Όμως αφού και το
και το
ανήκουν στο ίδιο ημιεπίπεδο ως προς την
έχουμε άτοπο.
Επομένως.
Πράγματι λοιπόν τα τρίγωνακαι
αποτελούν ζευγάρια ίσων τριγώνων.
Επομένως χρησιμοποιώντας και την (1) έχουμε ότι:
Άρα.
 ως προς το
ως προς το  .
. ως προς το
ως προς το  η λύση απλοποιείται κατά πολύ.
η λύση απλοποιείται κατά πολύ.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες