
- Διασταυρώνονται στον κύκλο.png (42.36 KiB) Προβλήθηκε 1060 φορές
Διαφορετικά:
Έστω ότι ο περιγεγραμμένος κύκλος του
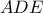
τέμνει την

στο

. Θα αποδείξουμε πως τα σημεία

είναι συνευθειακά, που ισοδυναμεί με το αρχικό πρόβλημα.
Θεωρούμε την αντιστροφή με πόλο το

και δύναμη

.
Παρατηρούμε πως το

πάει στο

, ενώ το

πάει στο

. Τονίζουμε ότι ο περιγεγραμμένος κύκλος του

παραμένει σταθερός μετά την αντιστροφή!
Φέρνουμε τον κύκλο αντιστροφής (είναι ο κύκλος με κέντρο

και ακτίνα

). Από την παραπάνω παρατήρηση προκύπτει ότι ο κύκλος της αντιστροφής και ο περιγεγραμμένος κύκλος του

είναι ορθογώνιοι.
Για δύο ορθογώνιους κύκλους ισχύει ότι η πολική ευθεία του κέντρου του ενός κύκλου στον άλλον κύκλο ταυτίζεται με την πολική ευθεία του άλλου κέντρου στον πρώτο κύκλο. Ειδικότερα η πολική ευθεία του

στον κύκλο της αντιστροφής ταυτίζεται με την πολική του

στον περιγεγραμμένο κύκλο του

.
Ισχύει ακόμα πως το αντίστροφο του

, έστω
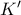
, είναι η τομή της

με την πολική του

στον κύκλο αντιστροφής. Άρα σύμφωνα με τα παραπάνω προκύπτει ότι το
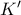
είναι η τομή της

με την πολική του

στον περιγεγραμμένο κύκλο του

. Μάλιστα η πολική αυτή θα τέμνει την

κάθετα.
Παρατηρούμε ακόμη πως o περιγεγραμμένος κύκλος του

γίνεται η

και αντίστροφα, ενώ ο περιγεγραμμένος κύκλος του
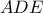
γίνεται η

.
Επομένως το αντίστροφο του

, έστω

, γίνεται η τομή των

και

.
Ακόμη το

γίνεται το

.
Ξέρουμε ότι το

ανήκει στην πολική του

ως προς τον περιγεγραμμένο κύκλο του

(γνωστό λήμμα).
Επομένως η πολική του

ως προς τον περιγεγραμμένο κύκλο του

είναι η

, η οποία είναι κάθετη λοιπόν στην

. Άρα
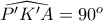
.
Προφανώς ισχύει ότι

, αφού το

είναι ύψος.
Επομένως το

είναι εγγράψιμο. Αφού τα αντίστροφα των

είναι ομοκυκλικά με τον πόλο

, θα ισχύει ότι τα

είναι συνευθειακά και το ζητούμενο έπεται.
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Στη πλευρά
. Στη πλευρά  κινείται σημείο
κινείται σημείο  .
. , που διέρχεται από τα σημεία
, που διέρχεται από τα σημεία  τέμνει , ακόμα , την
τέμνει , ακόμα , την  στο σημείο
στο σημείο  .
. που διέρχεται από τα σημεία
που διέρχεται από τα σημεία  τέμνει, ακόμα, τον κύκλο
τέμνει, ακόμα, τον κύκλο  στο σημείο
στο σημείο  .
. και το ύψος
και το ύψος  του
του  διασταυρώνονται πάνω στον κύκλο
διασταυρώνονται πάνω στον κύκλο  .
. εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Στη πλευρά
. Στη πλευρά  κινείται σημείο
κινείται σημείο  .
. , που διέρχεται από τα σημεία
, που διέρχεται από τα σημεία  τέμνει , ακόμα , την
τέμνει , ακόμα , την  στο σημείο
στο σημείο  .
. που διέρχεται από τα σημεία
που διέρχεται από τα σημεία  τέμνει, ακόμα, τον κύκλο
τέμνει, ακόμα, τον κύκλο  στο σημείο
στο σημείο  .
. και το ύψος
και το ύψος  του
του  διασταυρώνονται πάνω στον κύκλο
διασταυρώνονται πάνω στον κύκλο  .
. Ορίζουμε ως
Ορίζουμε ως  το ύψος του δοσμένου τριγώνου
το ύψος του δοσμένου τριγώνου  τον περίκυκλο του τριγώνου
τον περίκυκλο του τριγώνου  ( αντί του
( αντί του  της εκφώνησης ).
της εκφώνησης ). .
. είναι αντιπαράλληλες μεταξύ τους, ως προς τις ευθείες της γωνίας
είναι αντιπαράλληλες μεταξύ τους, ως προς τις ευθείες της γωνίας  και άρα, έχουμε
και άρα, έχουμε  όπου
όπου  είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  όπου
όπου  είναι το κέντρο του κύκλου
είναι το κέντρο του κύκλου  και επομένως, από
και επομένως, από  , προκύπτει ότι οι ευθείες
, προκύπτει ότι οι ευθείες  συντρέχουν στο σημείο έστω
συντρέχουν στο σημείο έστω  , ως το αντιδιαμετρικό σημείο του
, ως το αντιδιαμετρικό σημείο του  στον κύκλο
στον κύκλο  της εκφώνησης, ανήκει στην ευθεία
της εκφώνησης, ανήκει στην ευθεία  .
.

 κοινή χορδή των κύκλων
κοινή χορδή των κύκλων 
 , περνάει από το κέντρο
, περνάει από το κέντρο 

 , περνάει επίσης από το μέσον του τμήματος
, περνάει επίσης από το μέσον του τμήματος  , λόγω
, λόγω  , το ίδιο ίδιο όπως και η δια του σημείου
, το ίδιο ίδιο όπως και η δια του σημείου  .
. ταυτίζονται με τα ίχνη των αντίστοιχων υψών και το σημείο
ταυτίζονται με τα ίχνη των αντίστοιχων υψών και το σημείο  τέμνει την
τέμνει την  είναι συνευθειακά, που ισοδυναμεί με το αρχικό πρόβλημα.
είναι συνευθειακά, που ισοδυναμεί με το αρχικό πρόβλημα. .
. , ενώ το
, ενώ το  . Τονίζουμε ότι ο περιγεγραμμένος κύκλος του
. Τονίζουμε ότι ο περιγεγραμμένος κύκλος του  παραμένει σταθερός μετά την αντιστροφή!
παραμένει σταθερός μετά την αντιστροφή! ). Από την παραπάνω παρατήρηση προκύπτει ότι ο κύκλος της αντιστροφής και ο περιγεγραμμένος κύκλος του
). Από την παραπάνω παρατήρηση προκύπτει ότι ο κύκλος της αντιστροφής και ο περιγεγραμμένος κύκλος του  , είναι η τομή της
, είναι η τομή της  με την πολική του
με την πολική του  , γίνεται η τομή των
, γίνεται η τομή των  .
. , η οποία είναι κάθετη λοιπόν στην
, η οποία είναι κάθετη λοιπόν στην 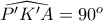 .
. , αφού το
, αφού το  είναι εγγράψιμο. Αφού τα αντίστροφα των
είναι εγγράψιμο. Αφού τα αντίστροφα των  η ακτίνα του κύκλου
η ακτίνα του κύκλου  το σημείο τομής του ύψους
το σημείο τομής του ύψους  Θα δείξω ότι τα σημεία
Θα δείξω ότι τα σημεία 
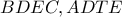 είναι
είναι  Άρα το
Άρα το 
 Αρκεί να δείξω ότι
Αρκεί να δείξω ότι 
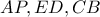 συντρέχουν στο ριζικό κέντρο
συντρέχουν στο ριζικό κέντρο  του εγγεγραμμένου
του εγγεγραμμένου είναι εγγράψιμο. Επομένως:
είναι εγγράψιμο. Επομένως:

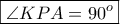 ( χαρακτηριστική ιδιότητα του
( χαρακτηριστική ιδιότητα του