Έστω

το κέντρο του κύκλου και

η ακτίνα του . Προφανώς


. Είναι :

Από Π. Θ. στο

έχω

. ενώ από τη δ΄τναμαη του

ως προς το κύκλο έχω

.
1.


- παιδεία εγκύκλου_new.png (24.72 KiB) Προβλήθηκε 500 φορές
2. Η τελευταία σχέση μας εξασφαλίζει ότι ,

.
Ας είναι

το σημείο τομής της

με την

Παίρνω τώρα Θ Μενελάου :
α) στο

με διατέμνουσα
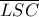
:

. Άρα

β) στο

με διατέμνουσα

:

Αλλά

. Οπότε

.
Αν τώρα

το άλλο σημείο τομής της

με τον κύκλο θα είναι :

. Δηλαδή το

είναι μέσο του

.
Αυτό έχει σαν συνέπεια να είναι :

άρα το

είναι αντιδιαμετρικό του

και

. Αφού όμως

θα είναι

.
Προφανώς τώρα η

διχοτομεί την ορθή γωνία

.
3. Αφού τώρα το τετράπλευρο

έχει τις γωνίες στα

ορθές είναι εγγράψιμο και έτσι :
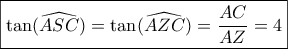
.
Πάμε παρακάτω.

- παιδεία εγκύκλου_new_extra.png (51.26 KiB) Προβλήθηκε 500 φορές
Ας είναι

το σημείο τομής της

με τη

.
Από Θ. Μενελάου στο

με διατέμνουσα

( ή λόγω αρμονικότητας της τετράδας

) έχω :

.

κι αυτό γιατί
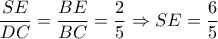
.
Ακόμη , Από Θ. Μενελάου στο

με διατέμνουσα

έχω :
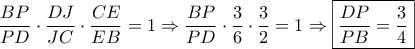
.
Τέλος έστω

το σημείο τομής του κύκλου με

. Επειδή το τραπέζιο

είναι ισοσκελές θα είναι:

. Αλλά αφού
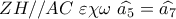
.
Έτσι τελικά :
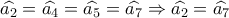
που μας εξασφαλίζει ότι το τετράπλευρο

είναι εγγράψιμο .
Στο άλλο με το σημείο

έχει απαντήσει
ο Γιώργος αλλά θα δω κι εγώ αν κάτι έχω να προσθέσω .
 , με κάθετες πλευρές
, με κάθετες πλευρές  σχεδιάσαμε
σχεδιάσαμε στο
στο  και τέμνεται από την
και τέμνεται από την  στο
στο  .
.



 σχεδιάσαμε
σχεδιάσαμε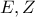 τα σημεία επαφής των
τα σημεία επαφής των  με τον κύκλο .
με τον κύκλο .  έχω
έχω  . Με δύναμη σημείου του
. Με δύναμη σημείου του  ως προς τον κύκλο έχω :
ως προς τον κύκλο έχω :  . Άρα
. Άρα  .
. έχω :
έχω :  . Ομοίως :
. Ομοίως : .
. . Ας είναι
. Ας είναι  η προβολή του
η προβολή του  έχω εύκολα:
έχω εύκολα:  Μετά απ’ αυτά :
Μετά απ’ αυτά :  και άρα
και άρα 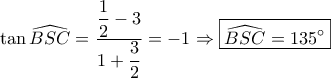 και
και 
 , μας ζητήσει και άλλα ερωτήματα
, μας ζητήσει και άλλα ερωτήματα  τέμνει τις
τέμνει τις  στα σημεία
στα σημεία 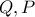
 και
και  .
. τέμνουν τον κύκλο και στα
τέμνουν τον κύκλο και στα  , δείξτε
, δείξτε είναι ομοκυκλικά ( συνεχίζεται ...)
είναι ομοκυκλικά ( συνεχίζεται ...) , τέμνονται στο
, τέμνονται στο  , τότε αφού αιτιολογήσετε
, τότε αφού αιτιολογήσετε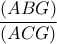 .
.
 από το
από το  σε ένα σημείο π.χ
σε ένα σημείο π.χ  όπου το
όπου το  χωρίζεται από
χωρίζεται από και είναι βαρύκεντρο του
και είναι βαρύκεντρο του  Δεν μπορώ πάντως να ξέρω τι έχει στο μυαλό του ο θεματοδότης.
Δεν μπορώ πάντως να ξέρω τι έχει στο μυαλό του ο θεματοδότης. 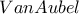 είναι
είναι 
 και
και  Έτσι έχουμε:
Έτσι έχουμε:

 το κέντρο του κύκλου και
το κέντρο του κύκλου και  η ακτίνα του . Προφανώς
η ακτίνα του . Προφανώς 
 . Είναι :
. Είναι : 
 . ενώ από τη δ΄τναμαη του
. ενώ από τη δ΄τναμαη του  .
.
 .
. το σημείο τομής της
το σημείο τομής της  με την
με την 
 με διατέμνουσα
με διατέμνουσα 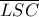 :
:  . Άρα
. Άρα 
 με διατέμνουσα
με διατέμνουσα  :
:
 . Οπότε
. Οπότε  .
. το άλλο σημείο τομής της
το άλλο σημείο τομής της  με τον κύκλο θα είναι :
με τον κύκλο θα είναι : . Δηλαδή το
. Δηλαδή το  .
. άρα το
άρα το  και
και  . Αφού όμως
. Αφού όμως  θα είναι
θα είναι  .
. διχοτομεί την ορθή γωνία
διχοτομεί την ορθή γωνία  .
. έχει τις γωνίες στα
έχει τις γωνίες στα  ορθές είναι εγγράψιμο και έτσι :
ορθές είναι εγγράψιμο και έτσι : 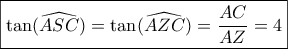 .
. με διατέμνουσα
με διατέμνουσα  ( ή λόγω αρμονικότητας της τετράδας
( ή λόγω αρμονικότητας της τετράδας  ) έχω :
) έχω :  .
. κι αυτό γιατί
κι αυτό γιατί 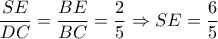 .
. με διατέμνουσα
με διατέμνουσα  έχω :
έχω :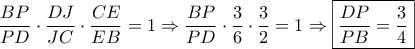 .
. το σημείο τομής του κύκλου με
το σημείο τομής του κύκλου με  . Επειδή το τραπέζιο
. Επειδή το τραπέζιο  είναι ισοσκελές θα είναι:
είναι ισοσκελές θα είναι:  . Αλλά αφού
. Αλλά αφού 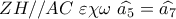 .
.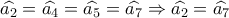 που μας εξασφαλίζει ότι το τετράπλευρο
που μας εξασφαλίζει ότι το τετράπλευρο  είναι εγγράψιμο .
είναι εγγράψιμο . έχει απαντήσει ο Γιώργος αλλά θα δω κι εγώ αν κάτι έχω να προσθέσω .
έχει απαντήσει ο Γιώργος αλλά θα δω κι εγώ αν κάτι έχω να προσθέσω . ...
...