 είναι το μέσο της πλευράς
είναι το μέσο της πλευράς  ισοσκελούς τριγώνου
ισοσκελούς τριγώνου  με
με  Γράφω τους κύκλους
Γράφω τους κύκλους και από το
και από το  φέρνω ευθεία που εφάπτεται στον κύκλο
φέρνω ευθεία που εφάπτεται στον κύκλο  στο
στο  και τέμνει τον κύκλο
και τέμνει τον κύκλο 
κατά σειρά στα σημεία
 Να δείξετε ότι
Να δείξετε ότι 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι το μέσο της πλευράς
είναι το μέσο της πλευράς  ισοσκελούς τριγώνου
ισοσκελούς τριγώνου  με
με  Γράφω τους κύκλους
Γράφω τους κύκλους και από το
και από το  φέρνω ευθεία που εφάπτεται στον κύκλο
φέρνω ευθεία που εφάπτεται στον κύκλο  στο
στο  και τέμνει τον κύκλο
και τέμνει τον κύκλο 
 Να δείξετε ότι
Να δείξετε ότι 
 τέμνει τον οριζόντιο άξονα στο
τέμνει τον οριζόντιο άξονα στο  . Με όμοια τρίγωνα :
. Με όμοια τρίγωνα :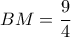 , άρα
, άρα  . Με τεμνόμενες χορδές :
. Με τεμνόμενες χορδές :  ,
, . Αλλά από Π.Θ. :
. Αλλά από Π.Θ. :  , συνεπώς και :
, συνεπώς και :  .
. το μέσο της χορδής
το μέσο της χορδής  θα είναι
θα είναι  . Έστω ακόμα
. Έστω ακόμα  τα μέσα των ακτίνων
τα μέσα των ακτίνων  .
. προφανώς είναι ρόμβος και τα τετράπλευρα
προφανώς είναι ρόμβος και τα τετράπλευρα  εγράψιμα σε ίσους κύκλους διαμέτρων
εγράψιμα σε ίσους κύκλους διαμέτρων  .
.  .
.  γιατί η εγγεγραμμένη είναι το μισό της αντίστοιχης επίκεντρης.
γιατί η εγγεγραμμένη είναι το μισό της αντίστοιχης επίκεντρης. ως εντός εναλλάξ των παραλλήλων
ως εντός εναλλάξ των παραλλήλων  με τέμνουσα
με τέμνουσα  .
. θα είναι
θα είναι  και αφού οι διαγώνιοι του ρόμβου τέμνονται κάθετα θα είναι
και αφού οι διαγώνιοι του ρόμβου τέμνονται κάθετα θα είναι 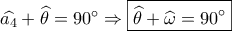
 εφάπτεται του κύκλου
εφάπτεται του κύκλου  .
. έχουν
έχουν 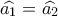 ( γιατί βαίνουν σε ίσα τόξα ίσων κύκλων ) θα είναι όμοια και άρα :
( γιατί βαίνουν σε ίσα τόξα ίσων κύκλων ) θα είναι όμοια και άρα : .
.  ως προς τους κύκλους ,
ως προς τους κύκλους ,  έχω ταυτόχρονα :
έχω ταυτόχρονα :
 έχω :
έχω :  άρα
άρα  οπότε η
οπότε η  δίδει :
δίδει :  , δηλαδή
, δηλαδή 
 στον κόκκινο κύκλο είναι
στον κόκκινο κύκλο είναι  , ενώ του
, ενώ του  στον μπλε κύκλο είναι
στον μπλε κύκλο είναι  . Αφού
. Αφού  , άρα το
, άρα το  έχει ίσες δυνάμεις ως προς τους δυο κύκλους, συνεπώς
έχει ίσες δυνάμεις ως προς τους δυο κύκλους, συνεπώς  .
.
 (1)
(1) ορίζεται ως το συμμετρικό του
ορίζεται ως το συμμετρικό του  ως προς την
ως προς την  . Έστω πως η
. Έστω πως η  τέμνει την
τέμνει την  στο
στο  . Παρατηρούμε ακόμα πως
. Παρατηρούμε ακόμα πως  .
.  , δηλαδή πως
, δηλαδή πως  .
.  σημείο της προέκτασης της
σημείο της προέκτασης της  προς το
προς το  με
με  , τότε το
, τότε το  ανήκει στον κόκκινο κύκλο, είναι δηλαδή
ανήκει στον κόκκινο κύκλο, είναι δηλαδή  .
.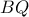 να είναι μεσοκάθετος του
να είναι μεσοκάθετος του  και αφού το
και αφού το  είναι ισοσκελές, αρκεί η
είναι ισοσκελές, αρκεί η 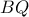 να διχοτομεί την
να διχοτομεί την  .
. και
και  , έχουμε πως το
, έχουμε πως το  είναι εγγράψιμο, άρα
είναι εγγράψιμο, άρα  .
. (2)
(2) το σημείο τομής του μπλε κύκλου με την
το σημείο τομής του μπλε κύκλου με την  . Έχουμε πως
. Έχουμε πως  . Άρα για να αποδείξουμε την (2) αρκεί να αποδείξουμε πως το σημείο που η
. Άρα για να αποδείξουμε την (2) αρκεί να αποδείξουμε πως το σημείο που η 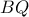 τέμνει την
τέμνει την  είναι το
είναι το  , δηλαδή πως για το σημείο τομής της
, δηλαδή πως για το σημείο τομής της 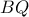 με την
με την  , έστω
, έστω  , ισχύει ότι ανήκει στο μπλε κύκλο, δηλαδή να είναι
, ισχύει ότι ανήκει στο μπλε κύκλο, δηλαδή να είναι  .
. με διατέμνουσα
με διατέμνουσα  πως
πως 
 με διατέμνουσα
με διατέμνουσα  και συνδυάζοντας την παραπάνω σχέση παίρνουμε πως
και συνδυάζοντας την παραπάνω σχέση παίρνουμε πως 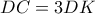 .
. με ύψος
με ύψος 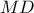 παίρνουμε πως
παίρνουμε πως  .
. και
και  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.Καλά Χριστούγεννα σε όλους.george visvikis έγραψε: ↑Τετ Δεκ 20, 2017 10:38 amΕφαπτόμενο τμήμα και χορδή.png
είναι το μέσο της πλευράς
ισοσκελούς τριγώνου
με
Γράφω τους κύκλους
και από το
φέρνω ευθεία που εφάπτεται στον κύκλο
στο
και τέμνει τον κύκλο
κατά σειρά στα σημείαΝα δείξετε ότι

 και
και  .Επειδή οι κύκλοι είναι ίσοι
.Επειδή οι κύκλοι είναι ίσοι  και
και  άρα
άρα  παραλ/μμο
παραλ/μμο κι από Π.Θ στο
κι από Π.Θ στο  έχουμε
έχουμε 

 διάμετρος και
διάμετρος και 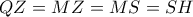 και οι κόκκινες γωνίες είναι ίσες ,άρα η
και οι κόκκινες γωνίες είναι ίσες ,άρα η  εφάπτεται του περίκυκλου του
εφάπτεται του περίκυκλου του 

Χωρίς βλάβη ( λόγω ομοιότητας ) , έστω :george visvikis έγραψε: ↑Τετ Δεκ 20, 2017 10:38 amείναι το μέσο της πλευράς
ισοσκελούς τριγώνου
με
Γράφω τους κύκλους
και από το
φέρνω ευθεία που εφάπτεται στον κύκλο
στο
και τέμνει τον κύκλο
κατά σειρά στα σημείαΝα δείξετε ότι

 , οπότε
, οπότε 
 . Η εξίσωση της εφαπτομένης του κύκλου
. Η εξίσωση της εφαπτομένης του κύκλου 
 , είναι η :
, είναι η :  και επειδή διέρχεται από το
και επειδή διέρχεται από το  , έχουμε :
, έχουμε : . Επίσης είναι :
. Επίσης είναι :  . Λύνοντας το σύστημα βρίσκουμε το
. Λύνοντας το σύστημα βρίσκουμε το  .
. . Είναι πλέον απλό
. Είναι πλέον απλό 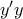 : θέτουμε
: θέτουμε  , οπότε :
, οπότε :  .
.  υπολογίζεται από την ομοιότητα των τριγώνων
υπολογίζεται από την ομοιότητα των τριγώνων  , (
, (  )
) με Π.Θ. . Στη συνέχεια η :
με Π.Θ. . Στη συνέχεια η : 
 , οπότε με αφαίρεση :
, οπότε με αφαίρεση : , άρα :
, άρα :  , ό.έ.δ.
, ό.έ.δ.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες