Σ' ευχαριστώ
Γιώργο για την ενασχόληση με το θέμα. Θα δώσω άλλη μία γεωμετρική κατασκευή που από ότι είδα δεν υπάρχει στις παραπομπές.
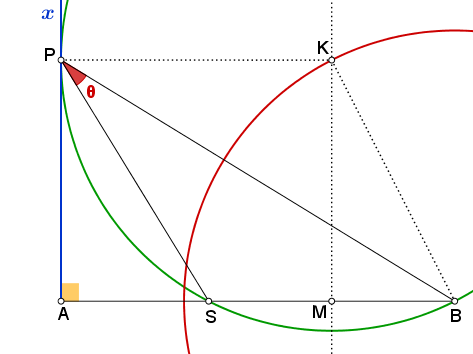
- Θέση μέγιστου.β.png (16.05 KiB) Προβλήθηκε 620 φορές
Ανάλυση: Έστω

το κέντρο του κύκλου που διέρχεται από τα σημεία

και

το μέσο του
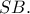
Για να είναι
η γωνία μέγιστη θα πρέπει, αφού το τμήμα

είναι σταθερό, η ακτίνα του κύκλου

να είναι ελάχιστη. Αυτό όμως
συμβαίνει όταν
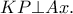
Προφανώς,
 Κατασκευή:
Κατασκευή: Γράφω τον κύκλο

που τέμνει τη μεσοκάθετο του

στο

και φέρνω από το

κάθετη στην

Το σημείο τομής τους είναι το ζητούμενο σημείο

 και ένα σημείο του
και ένα σημείο του  ώστε
ώστε 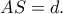 Φέρνω την ημιευθεία
Φέρνω την ημιευθεία 
 της
της  ώστε η γωνία
ώστε η γωνία  να είναι μέγιστη και (για αυτή τη θέση) να υπολογίσετε την
να είναι μέγιστη και (για αυτή τη θέση) να υπολογίσετε την 

 (ένα χρόνο πριν γίνω μέλος) και οι περισσότεροι σημερινοί μαθητές, αν όχι όλοι, σίγουρα δεν την έχουν συναντήσει εδώ! Ενδεχομένως κάπου αλλού, όχι όμως εδώ! Αυτό βέβαια πολύ λίγη σημασία έχει. Ας δούμε όμως τι αναφέρει η σχετική ανακοίνωση των Γενικών Συντονιστών:
(ένα χρόνο πριν γίνω μέλος) και οι περισσότεροι σημερινοί μαθητές, αν όχι όλοι, σίγουρα δεν την έχουν συναντήσει εδώ! Ενδεχομένως κάπου αλλού, όχι όμως εδώ! Αυτό βέβαια πολύ λίγη σημασία έχει. Ας δούμε όμως τι αναφέρει η σχετική ανακοίνωση των Γενικών Συντονιστών:  και
και  , με
, με  οπότε
οπότε 

 έχει παράγωγο
έχει παράγωγο  .
. .
. .
. είναι απλή. Φαίνεται στο σχήμα.
είναι απλή. Φαίνεται στο σχήμα. το κέντρο του κύκλου που διέρχεται από τα σημεία
το κέντρο του κύκλου που διέρχεται από τα σημεία  και
και  το μέσο του
το μέσο του 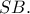 Για να είναι
Για να είναι είναι σταθερό, η ακτίνα του κύκλου
είναι σταθερό, η ακτίνα του κύκλου  να είναι ελάχιστη. Αυτό όμως
να είναι ελάχιστη. Αυτό όμως 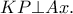 Προφανώς,
Προφανώς, 
 που τέμνει τη μεσοκάθετο του
που τέμνει τη μεσοκάθετο του 
