 , για την οποία υπάρχουν αριθμοί
, για την οποία υπάρχουν αριθμοί  , που ικανοποιούν την εξίσωση
, που ικανοποιούν την εξίσωση (
( πραγματικοί).
πραγματικοί).Συντονιστές: achilleas, emouroukos, silouan
 , για την οποία υπάρχουν αριθμοί
, για την οποία υπάρχουν αριθμοί  , που ικανοποιούν την εξίσωση
, που ικανοποιούν την εξίσωση (
( πραγματικοί).
πραγματικοί).ToAl.Koutsouridis έγραψε:Να βρείτε την ελάχιστη από τις τιμές του, για την οποία υπάρχουν αριθμοί
, που ικανοποιούν την εξίσωση
 είναι πραγματικός;
είναι πραγματικός;Ναι όλοι οι αριθμοί είναι πραγματικοί.Κατερινόπουλος Νικόλας έγραψε:
Toείναι πραγματικός;
 κάνουμε τον μετασχηματισμό
κάνουμε τον μετασχηματισμό  και η εξίσωση γίνεται
και η εξίσωση γίνεται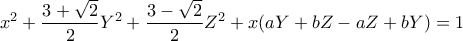
 ).
).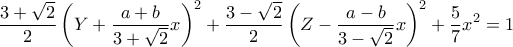
 )
) είναι
είναι  .
.Μετά την λύση του Δημήτρη δίνω μια πιο στοιχειώδη λύση.Al.Koutsouridis έγραψε:Να βρείτε την ελάχιστη από τις τιμές του, για την οποία υπάρχουν αριθμοί
, που ικανοποιούν την εξίσωση
(
πραγματικοί).


 με μεγιστοβάθμιο συντελεστή αρνητικό.
με μεγιστοβάθμιο συντελεστή αρνητικό.
 είναι
είναι 


 παίρνει μέγιστη και ελάχιστη τιμή.
παίρνει μέγιστη και ελάχιστη τιμή. σαν συνάρτηση των
σαν συνάρτηση των 

 και μετά ως προς
και μετά ως προς 
 είναι η μερική παράγωγος)
είναι η μερική παράγωγος)

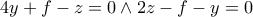

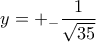

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες