Θα χρησιμοποιήσουμε το εξής λήμμα:Mihalis_Lambrou έγραψε: ↑Παρ Ιαν 12, 2018 4:09 pm
ΑΣΚΗΣΗ 27
Δείξτε ότι αν ο αριθμόςείναι πρώτος, τότε
για κάποιο φυσικό
.
Αν ο
 δε διαιρείται με το
δε διαιρείται με το  τότε το πολυώνυμο
τότε το πολυώνυμο  διαιρείται από το
διαιρείται από το 
Απόδειξη
Αν
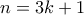 τότε
τότε  άρα
άρα 
διότι

Όμοια αν
 τότε
τότε  και παίρνουμε και πάλι ότι
και παίρνουμε και πάλι ότι 

Επιστρέφουμε στην άσκηση:
Από το παραπάνω λήμμα αν ο
 δεν διαιρείται από το
δεν διαιρείται από το  τότε για
τότε για  παίρνουμε ότι ο
παίρνουμε ότι ο  διαιρείται από το
διαιρείται από το  άρα δεν είναι πρώτος.
άρα δεν είναι πρώτος.Άρα για να είναι ο
 πρώτος πρέπει ο
πρώτος πρέπει ο  να διαιρείται από το
να διαιρείται από το  . Αν
. Αν  όπου
όπου  η μεγαλύτερη δύναμη του
η μεγαλύτερη δύναμη του  που υπάρχει στο
που υπάρχει στο  (δηλαδή
(δηλαδή  ) τότε με όμοιο επιχείρημα επειδή ο αριθμός
) τότε με όμοιο επιχείρημα επειδή ο αριθμός 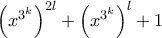 είναι πρώτος πρέπει ο
είναι πρώτος πρέπει ο  να διαιρείται από το
να διαιρείται από το  (από το παραπάνω Λήμμα), άτοπο. Άρα
(από το παραπάνω Λήμμα), άτοπο. Άρα  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε.Αλέξανδρος

 οι ρίζες της
οι ρίζες της  , να βρεθεί η τιμή της παράστασης
, να βρεθεί η τιμή της παράστασης  (άθροισμα κλασματικών μερών), χωρίς να επιλυθεί η εξίσωση.
(άθροισμα κλασματικών μερών), χωρίς να επιλυθεί η εξίσωση.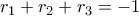 δηλαδή
δηλαδή ![[r_1]+[r_2]+[r_3]+\{r_1\}+\{r_2\}+\{r_3\}=-1 [r_1]+[r_2]+[r_3]+\{r_1\}+\{r_2\}+\{r_3\}=-1](/forum/ext/geomar/texintegr/latexrender/pictures/fd4f3ab57d60b7f9e5274893e6049617.png) και αφού ισχύει
και αφού ισχύει  άρα παίρνουμε
άρα παίρνουμε ![-4<[r_1]+[r_2]+[r_3]\leq -1 -4<[r_1]+[r_2]+[r_3]\leq -1](/forum/ext/geomar/texintegr/latexrender/pictures/af7e2a8edeaf543480c921f738171a21.png) .
.![[r_1]+[r_2]+[r_3] =-1 [r_1]+[r_2]+[r_3] =-1](/forum/ext/geomar/texintegr/latexrender/pictures/30650ec3dbd7c5a6f148ddf3034a8a60.png) τότε
τότε  κι έτσι
κι έτσι  , άτοπο αφού η αρχική εξίσωση δεν έχει ακέραιες ρίζες.
, άτοπο αφού η αρχική εξίσωση δεν έχει ακέραιες ρίζες.![[r_1]+[r_2]+[r_3]=-3 [r_1]+[r_2]+[r_3]=-3](/forum/ext/geomar/texintegr/latexrender/pictures/90a0437502ec59a2203fe4cd1e314372.png) τότε
τότε  . Αν ορίσουμε
. Αν ορίσουμε  , τότε αφού
, τότε αφού  ,
,  και
και  άρα για τις ρίζες ισχύει
άρα για τις ρίζες ισχύει  κι έτσι
κι έτσι  , άτοπο.
, άτοπο.![[r_1]+[r_2]+[r_3]=-2 [r_1]+[r_2]+[r_3]=-2](/forum/ext/geomar/texintegr/latexrender/pictures/e4fa4d8128a86cfee643921249696131.png) και τελικά
και τελικά  .
.![\{r_1\}+\{r_2\}+\{r_3\} = r_1+r_2+r_3- ([r_1]+[r_2]+[r_3])=-1- ([r_1]+[r_2]+[r_3]) \{r_1\}+\{r_2\}+\{r_3\} = r_1+r_2+r_3- ([r_1]+[r_2]+[r_3])=-1- ([r_1]+[r_2]+[r_3])](/forum/ext/geomar/texintegr/latexrender/pictures/9f5eff84c2a61ac4df588893cb70d4d4.png) . Τώρα, αφού για το δοθέν πολυώνυμο εύκολα υπολογίζουμε ότι
. Τώρα, αφού για το δοθέν πολυώνυμο εύκολα υπολογίζουμε ότι  , σημαίνει ότι έχει ρίζα
, σημαίνει ότι έχει ρίζα  . Άρα
. Άρα ![[r_1]=-3 [r_1]=-3](/forum/ext/geomar/texintegr/latexrender/pictures/43689f29acaa7f81ae2175d65f8c6a3b.png) . Όμοια για τις άλλες δύο ρίζες έχουμε
. Όμοια για τις άλλες δύο ρίζες έχουμε 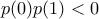 και
και  οπότε
οπότε  που σημαίνει
που σημαίνει ![[r_2]=-0, \, [r_3]=1 [r_2]=-0, \, [r_3]=1](/forum/ext/geomar/texintegr/latexrender/pictures/8f222ff43099cff2cd7f5582ed409922.png) . Τελικά
. Τελικά 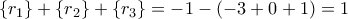
 είναι οι ρίζες του πολυωνύμου
είναι οι ρίζες του πολυωνύμου  να εκφράσετε την παράσταση
να εκφράσετε την παράσταση  συναρτήσει των
συναρτήσει των 

 με
με  και
και  . (Προφανώς οι
. (Προφανώς οι  είναι οι πρωταρχικές τέταρτες ρίζες του
είναι οι πρωταρχικές τέταρτες ρίζες του  και η μεταξύ τους σχέση είναι ότι
και η μεταξύ τους σχέση είναι ότι  )
) όπου το γινόμενο είναι πάνω στα
όπου το γινόμενο είναι πάνω στα  .
. βάλουμε όπου
βάλουμε όπου  το
το  παίρνουμε
παίρνουμε 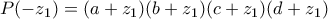 κ.ο.κ.
κ.ο.κ.
 ,
, ![P(z_2)=-qi+z_2(r-pi)\right]=\overline{\left[qi+z_1(r+pi)\right]}=\overline{P(z_1)} P(z_2)=-qi+z_2(r-pi)\right]=\overline{\left[qi+z_1(r+pi)\right]}=\overline{P(z_1)}](/forum/ext/geomar/texintegr/latexrender/pictures/56a6954a05b576995476456f59f8ee06.png) και τέλος
και τέλος
 και
και

 το πολυώνυμο
το πολυώνυμο  διαιρεί το
διαιρεί το  ;
; είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
.

![\displaystyle{n^3 [n^4 (n^2 -1)-(n^2 -1)-5(n^4 -2n^2 +1)]=n^3 [(n^2 -1)(n^4 -1)-5(n^2 -1)^2 ]=} \displaystyle{n^3 [n^4 (n^2 -1)-(n^2 -1)-5(n^4 -2n^2 +1)]=n^3 [(n^2 -1)(n^4 -1)-5(n^2 -1)^2 ]=}](/forum/ext/geomar/texintegr/latexrender/pictures/85c3ff736033e3c54780b44cf9bd14dd.png)
![\displaystyle{n^3 [(n^2 -1)^2 (n^2 +1)-5(n^2 -1)^2 ]= n^3 (n^2 -1)^2 (n^2 -4)=n^3 (n-1)^2 (n+1)^2 (n-2)(n+2)} \displaystyle{n^3 [(n^2 -1)^2 (n^2 +1)-5(n^2 -1)^2 ]= n^3 (n^2 -1)^2 (n^2 -4)=n^3 (n-1)^2 (n+1)^2 (n-2)(n+2)}](/forum/ext/geomar/texintegr/latexrender/pictures/175c1067cd8be6afee618297eab51c4d.png)
 , αρκεί να δείξουμε ότι ο αριθμός
, αρκεί να δείξουμε ότι ο αριθμός  διαιρείται με το
διαιρείται με το 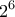 , το
, το 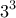 και το
και το  .
. , άρα θα διαιρείται με το 5 , αφού περιέχει γινόμενο πέντε διαδοχικών ακεραίων.
, άρα θα διαιρείται με το 5 , αφού περιέχει γινόμενο πέντε διαδοχικών ακεραίων. , άρα θα διαιρείται με το
, άρα θα διαιρείται με το 
 . Τότε
. Τότε 
 και άρα είναι πολλαπλάσιο του
και άρα είναι πολλαπλάσιο του  είναι πολλαπλάσιο του
είναι πολλαπλάσιο του 
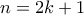 . Τότε
. Τότε 
 και άρα είναι πολλαπλάσιο του
και άρα είναι πολλαπλάσιο του  είναι
είναι  είναι οι ρίζες του πολυωνύμου
είναι οι ρίζες του πολυωνύμου  να υπολογίσετε την τιμή των παραστάσεων
να υπολογίσετε την τιμή των παραστάσεων

 ,
, .
. ,γίνεται
,γίνεται  .
. ,οπότε αν
,οπότε αν  ,θα είναι
,θα είναι  .
. ,δηλαδή
,δηλαδή 
 ,από όπου προκύπτει
,από όπου προκύπτει  ,από όπου γίνονται δεκτές και οι δύο λύσεις.(Αφού η
,από όπου γίνονται δεκτές και οι δύο λύσεις.(Αφού η  είναι κυκλική και όχι συμμετρική έχει σημασία η διάταξη των ριζών.Επιπλέον,αν πάρω τη μια από τις 2 για
είναι κυκλική και όχι συμμετρική έχει σημασία η διάταξη των ριζών.Επιπλέον,αν πάρω τη μια από τις 2 για  εξαιτίας της
εξαιτίας της  θα πάρει την άλλη κλπ.)
θα πάρει την άλλη κλπ.)
 και (επειδή
και (επειδή  ) η τρίτη είναι
) η τρίτη είναι  .
. 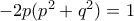 . Όμοια από το
. Όμοια από το  έπεται
έπεται  .
. . Προσπαθούμε τώρα να γράψουμε την παράσταση που βρήκαμε συναρτήσει των παραπάνω διώχνοντας τα
. Προσπαθούμε τώρα να γράψουμε την παράσταση που βρήκαμε συναρτήσει των παραπάνω διώχνοντας τα  . Εδώ τυχαίνει και είναι εύκολο, καθώς ισούται
. Εδώ τυχαίνει και είναι εύκολο, καθώς ισούται  .
. και
και  . Τώρα οι παραστάσεις
. Τώρα οι παραστάσεις  είναι συμμετρικές (εδώ είναι το κλειδί) και είναι εύκολο να τις βρούμε.
είναι συμμετρικές (εδώ είναι το κλειδί) και είναι εύκολο να τις βρούμε.  και
και 
 και
και  (εδώ διευκολύνει να πούμε ότι τα
(εδώ διευκολύνει να πούμε ότι τα  είναι ρίζες της
είναι ρίζες της 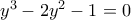 και λοιπά).
και λοιπά).  , που μαζί με την
, που μαζί με την  δίνει
δίνει 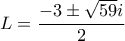 .
. είναι αναδιάταξη των
είναι αναδιάταξη των  ποιος είναι ο μικρότερος δυνατός βαθμός που μπορεί να έχει το πολυώνυμο
ποιος είναι ο μικρότερος δυνατός βαθμός που μπορεί να έχει το πολυώνυμο  ;
; με το
με το  .
.  Ακολουθούν το "μοτίβο":
Ακολουθούν το "μοτίβο":
 . Για να ισούται με
. Για να ισούται με 
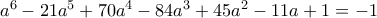
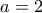 που είναι εύκολο να το αντιληφθούμε. Αν είναι μοναδική θα το ψάξω στο επόμενο ... τετράμηνο της Β' !!
που είναι εύκολο να το αντιληφθούμε. Αν είναι μοναδική θα το ψάξω στο επόμενο ... τετράμηνο της Β' !! ,
,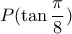 , ( εννοείται χωρίς χρήση λογισμικού ... )
, ( εννοείται χωρίς χρήση λογισμικού ... ) . Επειδή
. Επειδή  συμπεραίνουμε ότι το
συμπεραίνουμε ότι το  .
. 

 .
. όπου
όπου ![\displaystyle{f(x)\in \mathbb{Z}[x].} \displaystyle{f(x)\in \mathbb{Z}[x].}](/forum/ext/geomar/texintegr/latexrender/pictures/df537c31fdc8c35b94f6a91e3ef6d568.png)
 οπότε προκύπτει
οπότε προκύπτει


 απορρίπτονται γιατί τότε το
απορρίπτονται γιατί τότε το 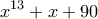 θα είχε δύο τουλάχιστον ρίζες (τις ρίζες του
θα είχε δύο τουλάχιστον ρίζες (τις ρίζες του 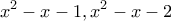 αντίστοιχα).
αντίστοιχα). γιατί αντιβαίνει στην
γιατί αντιβαίνει στην 
 Είναι εύκολο να δούμε ότι πράγματι
Είναι εύκολο να δούμε ότι πράγματι 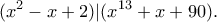
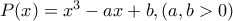 το οποίο έχει τρεις πραγματικές ρίζες. Να αποδείξετε ότι
το οποίο έχει τρεις πραγματικές ρίζες. Να αποδείξετε ότι