 με
με  , και έστω ένα σύνολο
, και έστω ένα σύνολο  από
από  διακεκριμένους ακεραίους. Έστω
διακεκριμένους ακεραίους. Έστω 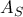 το σύνολο όλων των αριθμών που μπορούν να προκύψουν ως ο μέσος όρος δύο στοιχείων του
το σύνολο όλων των αριθμών που μπορούν να προκύψουν ως ο μέσος όρος δύο στοιχείων του  .
. Να βρεθεί το ελάχιστο δυνατό μέγεθος του
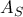 .
.Συντονιστές: Demetres, socrates, silouan
 με
με  , και έστω ένα σύνολο
, και έστω ένα σύνολο  από
από  διακεκριμένους ακεραίους. Έστω
διακεκριμένους ακεραίους. Έστω 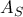 το σύνολο όλων των αριθμών που μπορούν να προκύψουν ως ο μέσος όρος δύο στοιχείων του
το σύνολο όλων των αριθμών που μπορούν να προκύψουν ως ο μέσος όρος δύο στοιχείων του  .
. 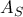 .
. που ανήκουν στο
που ανήκουν στο  , έτσι ώστε
, έτσι ώστε  .
. .
. σε πλήθος και είναι όλοι διαφορετικοί. Άρα το
σε πλήθος και είναι όλοι διαφορετικοί. Άρα το 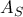 έχει αυτούς τους μέσους όρους τουλάχιστον, δηλαδή τουλάχιστον
έχει αυτούς τους μέσους όρους τουλάχιστον, δηλαδή τουλάχιστον  στοιχεία.
στοιχεία. , έτσι ώστε το πλήθος των στοιχείων του
, έτσι ώστε το πλήθος των στοιχείων του 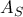 να είναι
να είναι  .
. (Μπορούμε και μια γενικότερη αριθμητική πρόοδο).
(Μπορούμε και μια γενικότερη αριθμητική πρόοδο). το σύνολο των μέσων όρων της μορφής
το σύνολο των μέσων όρων της μορφής  . Το πλήθος των στοιχείων του
. Το πλήθος των στοιχείων του  είναι
είναι  .
. με
με  , έχουμε πως αν
, έχουμε πως αν  , τότε
, τότε  , ο οποίος είναι μέσος όρος του
, ο οποίος είναι μέσος όρος του  . Αν
. Αν  , τότε
, τότε  , που ανήκει στο
, που ανήκει στο  .
. , άρα
, άρα  και πράγματι το
και πράγματι το 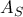 έχει
έχει  στοιχεία.
στοιχεία.Ωραία λύση.Διονύσιος Αδαμόπουλος έγραψε: ↑Τετ Ιαν 31, 2018 6:57 pmΘεωρούμε τους αριθμούςπου ανήκουν στο
, έτσι ώστε
.
Παρατηρούμε πως.
Αυτοί οι μέσοι όροι είναισε πλήθος και είναι όλοι διαφορετικοί.
 είναι με επαγωγή: Έστω
είναι με επαγωγή: Έστω  το ελάχιστο πλήθος, και ειδικά
το ελάχιστο πλήθος, και ειδικά  (άμεσο). Για το επαγωγικό βήμα, αν
(άμεσο). Για το επαγωγικό βήμα, αν  δοθέντες τότε πέρα από τους μέσους όρους των πρώτων
δοθέντες τότε πέρα από τους μέσους όρους των πρώτων  όρων έχουμε τουλάχιστον δύο καινούργιους όταν εξετάζουμε
όρων έχουμε τουλάχιστον δύο καινούργιους όταν εξετάζουμε  στοιχεία, τους
στοιχεία, τους 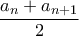 και
και  . Άρα
. Άρα  . Αναδρομικά,
. Αναδρομικά,  . Και λοιπά.
. Και λοιπά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες